Question

PQ is a post of height $a$, and A is a tower at some distance; $\alpha $and $\beta $ are the angles of elevation of B, the top of tower, at P and Q respectively. The height of the tower is

${\text{A}}{\text{. }}\dfrac{{a\sin \alpha \cos \beta }}{{\sin (\alpha - \beta )}}$
${\text{B}}{\text{. }}\dfrac{{a\cos \alpha \cos \beta }}{{\sin (\alpha - \beta )}}$
${\text{C}}{\text{. }}\dfrac{{a\sin \alpha \sin \beta }}{{\sin (\alpha - \beta )}}$
${\text{D}}{\text{.}}$ None of these

Answer 1

Hint: Draw the figure according to the information provided in the question and they analyse it to solve the question.

Complete step-by-step answer:

According to the question, PQ is a post of height a, and AB is the tower.
Let us assume the height of the tower be h.
The figure for the above question is shown below-

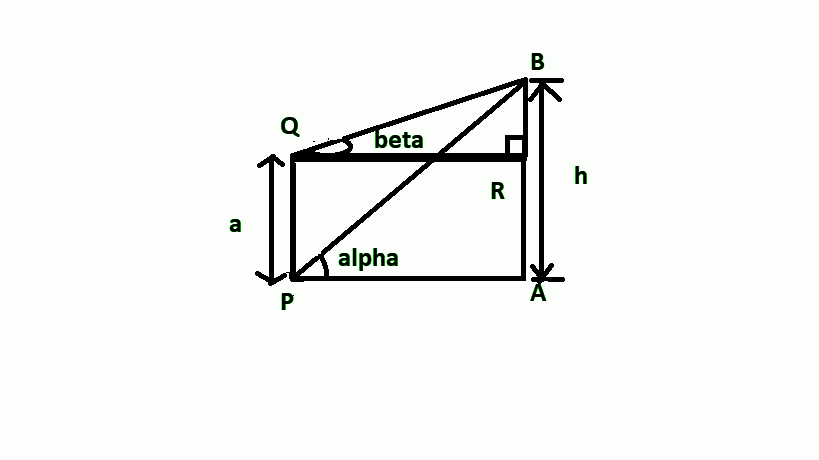
From the figure we can see,
PQ = AR = a.
Therefore, we can also say that, BR = AB -AR – (1)
Now, we know, AB = h (assume)
Therefore, substituting AB = h and AR = a in equation (1), we get-
$BR = h - a - (2)$
Now, in right angled triangle BAP,
$
  \tan \alpha = \dfrac{{AB}}{{AP}} \\
  \therefore \tan \alpha = \dfrac{h}{{AP}} \\
   \Rightarrow AP = \dfrac{h}{{\tan \alpha }} - (3) \\
$

Also, in right angle triangle BRQ,
$
  \tan \beta = \dfrac{{BR}}{{QR}} \\
  \therefore \tan \beta = \dfrac{{h - a}}{{AP}}[\because AP = RQ] \\
   \Rightarrow AP = \dfrac{{h - a}}{{\tan \beta }} - (4) \\
$

From equation (3) and (4), we can say,
$
  \dfrac{{h - a}}{{\tan \beta }} = \dfrac{h}{{\tan \alpha }} \\
   \Rightarrow h\tan \alpha - a\tan \alpha = h\tan \beta \\
   \Rightarrow h(\tan \alpha - \tan \beta ) = a\tan \alpha \\
   \Rightarrow h = \dfrac{{a\tan \alpha }}{{\tan \alpha - \tan \beta }} \\
$

We can write, $\tan \alpha = \dfrac{{\sin \alpha }}{{\cos \alpha }},\tan \beta = \dfrac{{\sin \beta }}{{\cos \beta }}$

So, h will be equal to, $
  h = \dfrac{{a\dfrac{{\sin \alpha }}{{\cos \alpha }}}}{{\dfrac{{\sin \alpha }}{{\cos \alpha }} - \dfrac{{\sin \beta }}{{\cos \beta }}}} = a\dfrac{{\sin \alpha }}{{\cos \alpha }} \times \dfrac{{\cos \alpha \cos \beta }}{{\sin \alpha \cos \beta - \cos \alpha \sin \beta }} \\
   \Rightarrow h = \dfrac{{a\sin \alpha \cos \beta }}{{\sin (\alpha - \beta )}} \\
$

Hence, the height of the tower is, $h = \dfrac{{a\sin \alpha \cos \beta }}{{\sin (\alpha - \beta )}}$.
Therefore, the correct option is A.


Note- Whenever such types of questions appear, always write the information given in the question, and using that make a figure, find the value of the tangent of angle $\alpha ,\beta $, and then solve further by making required substitutions.