Question

Plot the graph of ${{\sin }^{-1}}\left( \sin x \right)$ and write its domain and range.

Answer 1

Hint: To draw the graph of ${{\sin }^{-1}}\left( \sin x \right)$, we must know about the following concepts,
Inverse of a function means a function which returns back the original value applied on the given function. Inverse of a particular function exists if the function is bijective.i.e., for each unique value from the domain of the function, we should have a corresponding unique value from the range of the function.

Complete step-by-step solution:
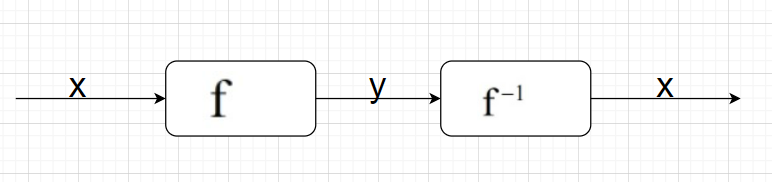
For a function $f$ , if its inverse exists, then
${{f}^{-1}}\left( f\left( x \right) \right)=x\text{ where }x\in Range\text{ of }{{f}^{-1}}\left( x \right)$
Another point to be noted is
$\begin{align}
  & \text{If, }\sin y=\sin x \\
 & \Rightarrow y=n\pi +{{\left( -1 \right)}^{n}}x \\
\end{align}$
Range of $y={{\sin }^{-1}}x$ $\forall x\in \left( -1,1 \right),y\in \left( \dfrac{-\pi }{2},\dfrac{\pi }{2} \right)$
Now, let us proceed with the question,
We have, $f\left( x \right)={{\sin }^{-1}}\left( \sin x \right)$
Let us assume $f\left( x \right)=\theta $
$\begin{align}
  & \Rightarrow {{\sin }^{-1}}\left( \sin x \right)=\theta \\
 & \Rightarrow \sin x=\sin \theta \\
\end{align}$
Using,
$\begin{align}
  & \text{If, }\sin y=\sin x \\
 & \Rightarrow y=n\pi +{{\left( -1 \right)}^{n}}x \\
\end{align}$
We get
$\Rightarrow \theta =n\pi +{{\left( -1 \right)}^{n}}x$
For different values of $x$ , we will get different values of $\theta $ .i.e., for different values of $x$, we will get different values of $f\left( x \right)$ .
For $n=-1$
$\theta ={{\sin }^{-1}}\left( \sin \left( -\pi -x \right) \right)$
For $\theta $ to exist,
$\begin{align}
  & \dfrac{-\pi }{2}\le -\pi -x\le \dfrac{\pi }{2} \\
 & \Rightarrow \dfrac{\pi }{2}\le -x\le \dfrac{3\pi }{2} \\
 & \Rightarrow \dfrac{-\pi }{2}\ge x\ge \dfrac{-3\pi }{2} \\
\end{align}$
For $n=0,$
$\theta ={{\sin }^{-1}}\left( \sin x \right)$
For $\theta $ to exist,
$\dfrac{-\pi }{2}\le x\le \dfrac{\pi }{2}$
For $n=1,$
$\theta ={{\sin }^{-1}}\left( \sin \left( \pi -x \right) \right)$
For $\theta $ to exist,
$\begin{align}
  & \dfrac{-\pi }{2}\le \pi -x\le \dfrac{\pi }{2} \\
 & \Rightarrow \dfrac{-3\pi }{2}\le -x\le \dfrac{-\pi }{2} \\
 & \Rightarrow \dfrac{3\pi }{2}\ge x\ge \dfrac{\pi }{2} \\
\end{align}$
So, we can redefine the function $f\left( x \right)$ as
$f\left( x \right)=\left\{ \begin{matrix}
  & -\pi -x &\dfrac{-3\pi }{2}\le x\le \dfrac{-\pi }{2} \\
 & x & \dfrac{-\pi }{2}\le x\le \dfrac{\pi }{2} \\
 & \pi -x & \dfrac{\pi }{2}\le x\le \dfrac{3\pi }{2} \\
\end{matrix} \right.$
Now, using these inequalities we will draw the graph of $f\left( x \right)={{\sin }^{-1}}\left( \sin x \right)$

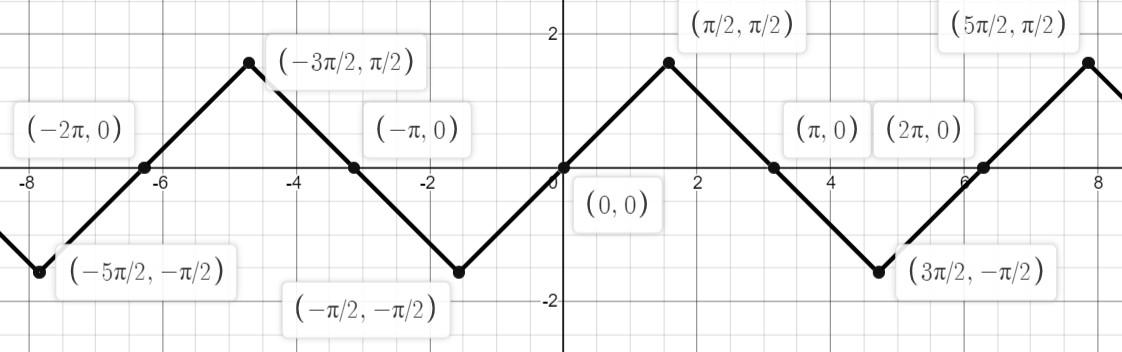
So, for the function $f\left( x \right)={{\sin }^{-1}}\left( \sin x \right)$
$Domain:x\in R$
$Range:x\in \left( \dfrac{-\pi }{2},\dfrac{\pi }{2} \right)$
The graph is periodic with a fundamental period of $2\pi $.

Note: While drawing the graph of $f\left( x \right)={{\sin }^{-1}}\left( \sin x \right)$, remember that the different values of $x$ should correspond to the range of ${{\sin }^{-1}}x$ .i.e.,$x\in \left( \dfrac{-\pi }{2},\dfrac{\pi }{2} \right)$. Here, since $x$ is the domain of $\sin x$, hence $x\in R$. This means that $\sin x\in \left( -1,1 \right)$ and hence ${{\sin }^{-1}}\left( \sin x \right)\in \left( \dfrac{-\pi }{2},\dfrac{\pi }{2} \right)$. So, the given function has a range of $\left( \dfrac{-\pi }{2},\dfrac{\pi }{2} \right)$ for every $x\in R$.