
How do you plot the following graph $ x=\sqrt{y-1} $ ?
Answer
562.8k+ views
Hint: In this question, we need to plot the graph for the given equation $ x=\sqrt{y-1} $ . For this, we will take square both sides and graph for $ y={{x}^{2}}+1 $ . We will suppose some points for x and find values of y. Using the points, we will plot the graph for $ y={{x}^{2}}+1 $ which will be a parabola.
Complete step by step answer:
Here we are given the equation of the function as $ x=\sqrt{y-1} $ .
We need to draw its graph. For this let us first simplify the equation,
Squaring both sides we get $ {{x}^{2}}={{\left( \sqrt{y-1} \right)}^{2}}\Rightarrow {{x}^{2}}=y+1 $ .
Taking 1 to the other side we get $ y={{x}^{2}}+1 $ .
We need to draw a graph for this equation.
As $ {{x}^{2}} $ is positive and it is in the quadratic form so our graph shape will be an upward parabola $ \left( \bigcup \right) $ . In general form, $ y=a{{x}^{2}}+bx+c $ the bx part of the equation shifts graph left or right but here we do not have, so our graph is central about the y-axis. Since the C part is +1 so the general parabola will shift upward.
Let us find some points to plot the graph,
Taking x = 0 we get $ y={{\left( 0 \right)}^{2}}+1\Rightarrow y=1 $ .
Taking x = 1 we get $ y={{\left( 1 \right)}^{2}}+1\Rightarrow y=2 $ .
Taking x = 2 we get $ y={{\left( 2 \right)}^{2}}+1\Rightarrow y=5 $ .
Taking x = 3 we get $ y={{\left( 3 \right)}^{2}}+1\Rightarrow y=10 $ .
Taking x = -1 we get $ y={{\left( -1 \right)}^{2}}+1\Rightarrow y=2 $ .
Taking x = -2 we get $ y={{\left( -2 \right)}^{2}}+1\Rightarrow y=5 $ .
Taking x = -3 we get $ y={{\left( -3 \right)}^{2}}+1\Rightarrow y=10 $ .
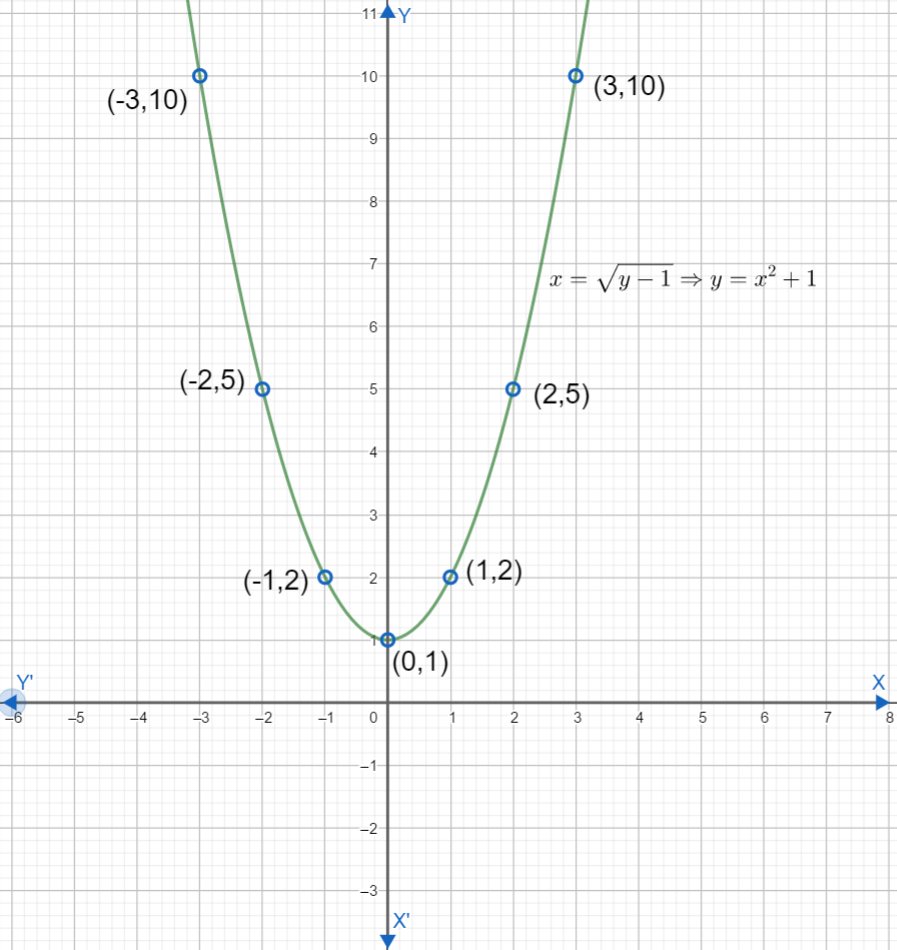
So our table of points that we will plot looks like this,
Now, let us draw the y-axis as a vertical line and x-axis as the horizontal line and mark the variables O, X, Y. Let us mark relevant points for the x and y-axis. Now let us plot all the points.
After this, let us draw a smooth curve passing through these points. This graph is our final answer.
Note:
Students should always try to find a point for the negative x-axis too because as observed earlier, this parabola is centered along the y-axis. Note that for any value of x, y cannot be negative because the equation involves $ {{x}^{2}} $ only. Make sure to make a smooth curve for more accuracy, students can plot more points.
Complete step by step answer:
Here we are given the equation of the function as $ x=\sqrt{y-1} $ .
We need to draw its graph. For this let us first simplify the equation,
Squaring both sides we get $ {{x}^{2}}={{\left( \sqrt{y-1} \right)}^{2}}\Rightarrow {{x}^{2}}=y+1 $ .
Taking 1 to the other side we get $ y={{x}^{2}}+1 $ .
We need to draw a graph for this equation.
As $ {{x}^{2}} $ is positive and it is in the quadratic form so our graph shape will be an upward parabola $ \left( \bigcup \right) $ . In general form, $ y=a{{x}^{2}}+bx+c $ the bx part of the equation shifts graph left or right but here we do not have, so our graph is central about the y-axis. Since the C part is +1 so the general parabola will shift upward.
Let us find some points to plot the graph,
Taking x = 0 we get $ y={{\left( 0 \right)}^{2}}+1\Rightarrow y=1 $ .
Taking x = 1 we get $ y={{\left( 1 \right)}^{2}}+1\Rightarrow y=2 $ .
Taking x = 2 we get $ y={{\left( 2 \right)}^{2}}+1\Rightarrow y=5 $ .
Taking x = 3 we get $ y={{\left( 3 \right)}^{2}}+1\Rightarrow y=10 $ .
Taking x = -1 we get $ y={{\left( -1 \right)}^{2}}+1\Rightarrow y=2 $ .
Taking x = -2 we get $ y={{\left( -2 \right)}^{2}}+1\Rightarrow y=5 $ .
Taking x = -3 we get $ y={{\left( -3 \right)}^{2}}+1\Rightarrow y=10 $ .
So our table of points that we will plot looks like this,
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | 10 | 5 | 2 | 1 | 2 | 5 | 10 |
Now, let us draw the y-axis as a vertical line and x-axis as the horizontal line and mark the variables O, X, Y. Let us mark relevant points for the x and y-axis. Now let us plot all the points.
After this, let us draw a smooth curve passing through these points. This graph is our final answer.

Note:
Students should always try to find a point for the negative x-axis too because as observed earlier, this parabola is centered along the y-axis. Note that for any value of x, y cannot be negative because the equation involves $ {{x}^{2}} $ only. Make sure to make a smooth curve for more accuracy, students can plot more points.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

A moving boat is observed from the top of a 150 m high class 10 maths CBSE




