Question

Plot a graph showing the variation of acceleration due to gravity with the distance from the centre of the earth.

Answer 1

Hint:We have to take distance from earth on the x-axis as it is an independent value, and acceleration due to gravity on y-axis as it is dependent on the distance from the centre of the earth for this graph.

Complete step by step solution:
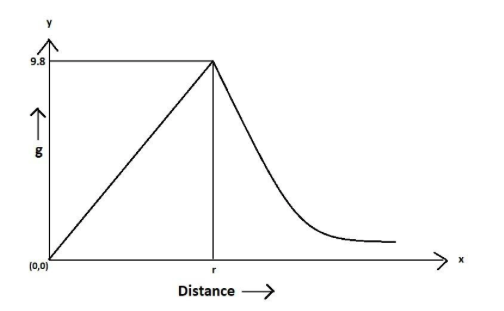
We need to plot this graph between two quantities – distance and acceleration due to gravity, called $g$. Since acceleration due to gravity is a dependent function, being dependent on distance from the centre of the earth, it will be plotted over the y-axis and distance, being an independent quantity, will be plotted over the x-axis.

We need to take the centre of the earth as a reference for measuring distance, as given in the question. This means that the centre of the earth will be taken as an initial distance. In other words, at the centre of the earth, distance will be equal to zero. Also, we know that at the centre of the earth acceleration due to gravity is zero. Therefore, we get the coordinates $\left( {0,0} \right)$ to satisfy the graph, indicating that at the centre of the earth acceleration due to gravity will be zero.

Now, we know that the value of acceleration due to gravity on the surface of the earth, i.e. at a distance equal to the radius of the earth, is equal to $9.8\,m{s^{ - 2}}$ and also that the value of the acceleration due to gravity is highest at a distance equal to the radius of the earth. Hence, if we take the radius of the earth to be $r$, we get the point $(r,9.8)$ for our graph.

Now, it has been proven that the acceleration due to gravity increases uniformly till a distance equal to the radius of the earth, where it becomes highest, and then decreases exponentially. Hence, from the origin to the point $(r,9.8)$ graph will be a straight line and after the point $(r,9.8)$ the graph will decrease exponentially, tending to zero as distance tends to infinity.
Therefore, the graph will be as below:

Note:It has been scientifically proven that acceleration due to gravity increases uniformly till a distance equal to the radius of the earth, where it becomes highest, and then decreases exponentially. The acceleration due to gravity never becomes zero. No matter how far we go from earth, there will always be some of it acting on us except for when we reach the centre of earth, where it becomes zero.