Question

Places A and B are 80 km apart from each other on a highway. A car starts from A and another from B at the same time. If they move in the same direction, they meet in 8 hours and if they move towards each other they meet in 1 hour and 20 minutes. Find the speed of the cars.

Answer 1

Hint: To solve this question, we will first assume the speeds of the cars to be x km/h and y km/h. Then we will find the distance covered by both the cars in both the cases in terms of the time taken and the speed they are traveling at which and then we will use the distances to form two equations in x and y. Then we will solve both those equations simultaneously and hence obtain the value of x and y. Thus, we will get an answer.

Complete step-by-step solution
Here first, let us assume the speed of the car starting from A to be x km/h and that of the car starting from B to be y km/h.
Hence, we have to find the value of x and y.
Now, in the first condition, we have been given that when the cars move in the same direction, they meet in 8 hours.
Let us assume they meet at point C. We have also been given that A and B are 80 km apart.
Thus, we can say that:
AB=80 km

Now, from the figure, we can see that:
AC-BC=AB …..(i)
We also know that the AC is the distance covered by the car starting from A in 8 hours and BC is the distance covered by the car starting from B in 8 hours.
We also know that the distance ‘d’ covered by an object in time ‘t’ traveling through a speed ‘s’ is given as:
$d=st$
Now, the speed of the car starting at A is x and the distance covered by it in 8 hours is AC. Thus, we can say that:
$AC=8x$
Similarly, the speed of the car starting at B is y, and the distance covered by it in 8 hours in BC. Thus, we can say that:
$BC=8y$
Now, putting the values of AC and BC in equation (i) we get:
$\begin{align}
  & AC-BC=AB \\
 & \Rightarrow 8x-8y=80 \\
\end{align}$
Taking 8 commons on the LHS of this equation we get:
$\begin{align}
  & 8x-8y=80 \\
 & \Rightarrow 8\left( x-y \right)=80 \\
\end{align}$
$\Rightarrow x-y=10$ …..(ii)
Now, the second condition given to us is that when they move towards each other, they meet in 1 hour 20 minutes.
Now, we know that 20 minutes can be written in the form of hours as:
$\begin{align}
  & \dfrac{20}{60}hours \\
 & \Rightarrow \dfrac{1}{3}hours \\
\end{align}$
Hence, the total time will be:
$\begin{align}
  & 1\text{hours}+20\text{minutes} \\
 & \Rightarrow \left( 1+\dfrac{1}{3} \right)hours \\
 & \Rightarrow \dfrac{4}{3}hours \\
\end{align}$
Now let us assume that they meet at the point D.

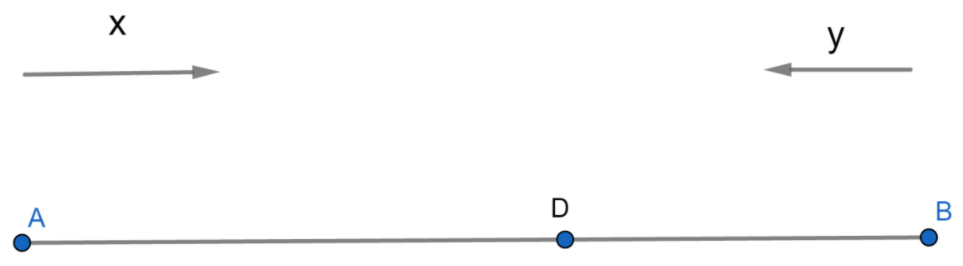
Now, from the figure we can see that:
AD+BD=AB …..(iii)
Now, the car starting from point A travels a distance AD in time $\dfrac{4}{3}$ hours with speed x km/h. Thus, we can say that:
$AD=\dfrac{4}{3}x$
Similarly, the car starting from point B travels a distance BD in time $\dfrac{4}{3}$ hours with the speed y km/h. Thus, we can say that:
$BD=\dfrac{4}{3}y$
Now, putting the values of AD and BD in equation (iii) we get:
$\begin{align}
  & AD+BD=AB \\
 & \Rightarrow \dfrac{4}{3}x+\dfrac{4}{3}y=80 \\
\end{align}$
Now, taking $\dfrac{4}{3}$ common from the LHS of this equation we get:
$\begin{align}
  & \dfrac{4}{3}x+\dfrac{4}{3}y=80 \\
 & \Rightarrow \dfrac{4}{3}\left( x+y \right)=80 \\
\end{align}$
$\Rightarrow x+y=60$ …..(iv)
Now, we have the equations (ii) and (iv) as:
$\begin{align}
  & x-y=10 \\
 & x+y=60 \\
\end{align}$
Now, solving these equation simultaneously we get:
$\begin{align}
  & x+y=60 \\
 & \underline{x-y=10} \\
 & \underline{\ \ 2x=70\ } \\
 & \Rightarrow x=\dfrac{70}{2} \\
 & \therefore x=35 \\
\end{align}$
Now, putting the value of x in equation (ii) we get:
$\begin{align}
  & x-y=10 \\
 & \Rightarrow 35-y=10 \\
 & \therefore y=25 \\
\end{align}$
Hence, the values of x and y are 35 km/h and 25 km/h respectively.
Thus, the speed of the car starting at point A is 35 km/h and that of the car starting from B is 25 km/h.

Note: Be careful while forming the relationships between x and y here as any mistake in that will result in a wrong equation and hence will result in the wrong solution for the equations. Also, be careful while solving the equations. Here, we have used the elimination method to solve the equations but we can use the substitution method or the cross multiplication method according to our convenience.