What is the phase angle in a series RLC circuit at resonance?
A) $180^{0}$
B) $90^{0}$
C) $0^{0}$
D) $- 90^{0}$
E) None of the above

Question

What is the phase angle in a series RLC circuit at resonance?A) ${180^0}$B) ${90^0}$C) ${0^0}$D) $ - {90^0}$E) None of the above

Vedantu Content Team · Accepted Answer

Hint: A series RLC is an AC circuit that is said to be in electrical resonance when the circuit power factor is unity i.e., ${X_L} = {X_C}$. Where ${X_L}$ and ${X_C}$ are inductive reactance and capacitive reactance respectively.The phase angle in a RLC circuit is given by $\phi  = {\tan ^{ - 1}}\left( {\dfrac{{{X_L} - {X_C}}}{R}} \right)$. Where $R$ is the resistance.Complete step by step answer:Let’s draw an AC circuit containing resistor, inductor and capacitor in series. $E$ and $I$ are the e.m.f. and current in the circuit respectively.

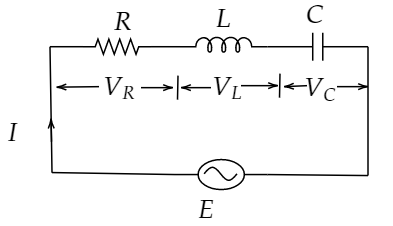
The voltage across resistor $\left( R \right)$, ${V_R} = IR$${V_R}$ is in phase with $I$.The voltage across inductor $\left( L \right)$, ${V_L} = I{X_L}$${V_L}$ leads $I$ by ${90^0}$.The voltage across capacitor $\left( C \right)$, ${V_C} = I{X_C}$${V_C}$ lags $I$ by ${90^0}$.Consider ${V_L} > {V_C}$. Now draw the phasor diagram.

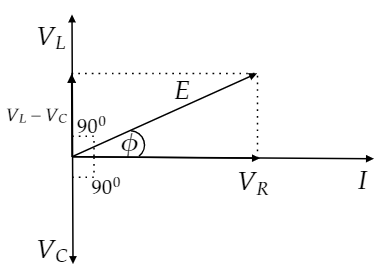
The resultant voltage in the phasor diagram is the applied voltage and it is given by$E = \sqrt {{V_R}^2 + {{\left( {{V_L} - {V_C}} \right)}^2}} $Or $E = \sqrt {{{\left( {IR} \right)}^2} + {{\left( {I{X_L} - I{X_C}} \right)}^2}} $Or $ I = \dfrac{E}{{\sqrt {{R^2} + {{\left( {{X_L} - {X_C}} \right)}^2}} }}$The quantity $Z = \sqrt {{R^2} + {{\left( {{X_L} - {X_C}} \right)}^2}} $ is called impedance of the circuit.The angle $\phi $ in the above phasor diagram is known as phase angle in the circuit.$\tan \phi  = \dfrac{{{V_L} - {V_C}}}{{{V_R}}}$Or $\tan \phi  = \dfrac{{{X_L} - {X_C}}}{R}$Or $ \Rightarrow \phi  = {\tan ^{ - 1}}\left( {\dfrac{{{X_L} - {X_C}}}{R}} \right)$At resonance, the impedance of the circuit is minimum and is equal to the resistance of the circuit.i.e., $Z = R$Or $\sqrt {{R^2} + {{\left( {{X_L} - {X_C}} \right)}^2}}  = R$Further simplify$ \Rightarrow {X_L} = {X_C}$Now at resonance, phase angle $\phi  = {\tan ^{ - 1}}\left( 0 \right)$Or $\phi  = {0^0}$Hence, the correct option is (C) ${0^0}$.Note: Alternative  method for solving the problem:When the RLC series AC circuit is at resonance, the average power in the circuit is maximum.$P = {E_{rms}}{I_{rms}}\cos \phi $. Where ${E_{rms}}$ and ${I_{rms}}$ are the rms values of voltage and current in the circuit.$co\phi $ is called the power factor of the circuit.At resonance, $P = {E_{rms}}{I_{rms}}$Therefore, $\cos \phi  = 1$Or $\phi  = {0^0}$

What is the phase angle in a series RLC circuit at resonance?A) 1800B) 900C) 00D) −900E) None of the above

Repeaters Course for NEET 2022 - 23

What is the phase angle in a series RLC circuit at resonance?
A) $180^{0}$
B) $90^{0}$
C) $0^{0}$
D) $- 90^{0}$
E) None of the above