Question

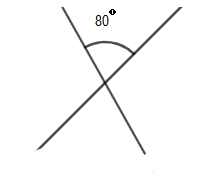
What is the order of the rotational symmetry of the given figure?

Answer 1

Hint: Think of the basic definition of the line of symmetry and the property that line of symmetry acts as a plane mirror such that one side of the body is that object and the other side is the image of the object. If needed, a diagram could also be used for better visualisation. For a better visualisation it is better to use the concept of vertically opposite angles to find the one other angle as well.

Complete step-by-step answer:
Before starting with the solution, let us discuss the elements of symmetry and when a body is said to be symmetric or asymmetric. First, we will discuss the two major elements of symmetry, which are the line of symmetry and axis of symmetry.
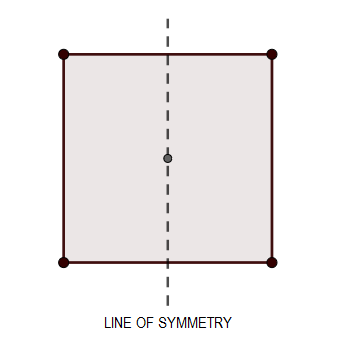
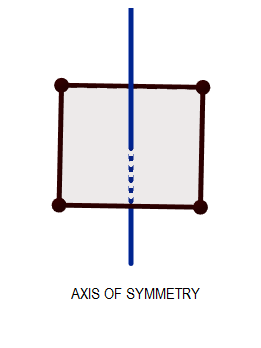
The "Line of Symmetry" is the imaginary line through the body, which divides the body into two equal halves such that the parts on each side of the body are the mirror images of each other. While the axis of symmetry is an axis passing through the body about which the rotation of the body gives the exact identical figure as the initial one, provided the angle of rotation is less than , and the number of times the figure is repeated while rotating it by is the order of the rotational symmetry.
If a body consists of at least one of the elements of symmetry mentioned above is said to be symmetric. We can represent this diagrammatically as:

Now let us start the solution to the above question by drawing the diagram of the situation given in the figure.

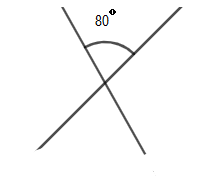
Now if we use the concept of vertically opposite angles, we get

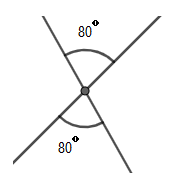
Now, if we rotate the figure by $180{}^\circ $ about the axis passing through the centre marked in the figure and perpendicular to the plane of the paper, we will find the figure we get is exactly the same as the figure given. So, for every $180{}^\circ $ rotation, we get the same identical figure. Therefore, we can say that the order of rotational symmetry is equal to $\dfrac{360{}^\circ }{180{}^\circ }$ , which is equal to 2.

Note: Remember that it is possible that a figure can have multiple elements of symmetry. For example: a circle has an infinite number of lines of symmetry and one axis of rotational symmetry with infinite order of rotational symmetry. It is better if you remember the properties of different pairs of angles: linear pair, vertically opposite angles etc.