
One mole of a monatomic ideal gas undergoes a cyclic process as shown in the figure (where V is the volume and T is the temperature). Which of the statements below is (are) true?
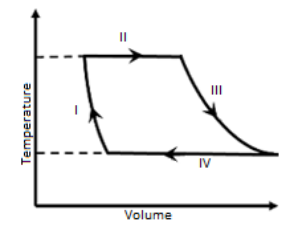
A. Process I is an Isochoric process.
B. In process II, gas absorbs heat.
C. In process IV, gas releases heat.
D. Process I and II are not Isobaric.

Answer
566.4k+ views
Hint:As stated, a monatomic ideal gas is undergoing a cyclic process that means the initial and final state of the system will be the same and also the initial and final energies will be the same. Hence, the internal energy change will be zero for a cyclic process. This also implies that the heat absorbed by the system will be the same as that of work done by the system during the cyclic process.
Complete answer:
To answer this question, we need to first understand the diagram given in the question.
The diagram given is a volume-temperature diagram for a cyclic process and from the diagram, we can observe that the volume, V of the monatomic ideal gas varies with temperature, T.
In thermodynamics, when a system is taken from initial to final stage, it can happen by different processes. Let us understand some of these processes.A process is said to be isothermal if the temperature of the system remains constant. In an isothermal process, internal energy change will be zero as internal energy of the system depends upon the temperature.
The isobaric process is a process in which the pressure of the system remains constant, whereas during an isochoric process the volume of the system will remain constant.
Let us observe process I, both temperature and volume change is taking place. As shown in the diagram, volume of the gas is decreasing during process I. Therefore, the process I is not isochoric as volume of the gas does not remain constant. Hence, option (A) is incorrect.
Now, let us observe the given diagram, we can see that both processes II and IV are depicted as a straight line.Therefore, both processes II and IV are isothermal.
During process II, the volume of the gas is increasing and temperature remains constant so it is an isothermal expansion. Hence, from 1st law of thermodynamics, we can deduce that,
$[Q = \Delta U + W]$
Here, $[Q]$ is net heat transfer in the system, $[\Delta U]$ is a change in internal energy of the system and $[W]$ is the total work done by the system.
Here, $[\Delta U = 0]$, $[W > 0]$
Therefore, $[Q > 0]$, hence in process II heat gets absorbed. So, option B is correct.
Again, process IV is isothermal compression, as the volume of gas is decreasing at constant temperature during the process. Hence, by 1st law of thermodynamics,
$[W < 0]$ and $[\Delta U = 0]$
Therefore the heat is released in this process as $[Q < 0]$. Hence, option C is also correct.
In an isobaric process, the pressure of the system does not change and temperature will be directly proportional to volume.
$[\therefore T\alpha V]$
In other words, if processes I and II would have been isobaric, then the Volume-Temperature graph should be of straight line. But, it is not true. Hence, process I and II are not isobaric.Hence, option D is correct.
Therefore, the correct options are options B, C and D.
Note:According to the first law of thermodynamics, the change in internal energy of a system is the same as that of the difference between the net heat transfer in the system and net work done by the system.
Mathematically, it can be expressed as,
$[\Delta U = Q - W]$
Here, $[Q]$ is net heat transfer in the system, $[\Delta U]$ is a change in internal energy of the system and $[W]$ is the total work done by the system.
If the value of Q is positive, then energy is added to the system and if W is positive the energy will be taken from the system by work.
Complete answer:
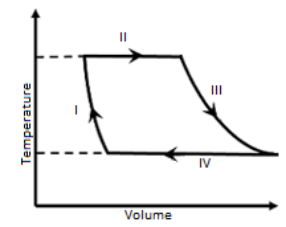
To answer this question, we need to first understand the diagram given in the question.
The diagram given is a volume-temperature diagram for a cyclic process and from the diagram, we can observe that the volume, V of the monatomic ideal gas varies with temperature, T.

In thermodynamics, when a system is taken from initial to final stage, it can happen by different processes. Let us understand some of these processes.A process is said to be isothermal if the temperature of the system remains constant. In an isothermal process, internal energy change will be zero as internal energy of the system depends upon the temperature.
The isobaric process is a process in which the pressure of the system remains constant, whereas during an isochoric process the volume of the system will remain constant.
Let us observe process I, both temperature and volume change is taking place. As shown in the diagram, volume of the gas is decreasing during process I. Therefore, the process I is not isochoric as volume of the gas does not remain constant. Hence, option (A) is incorrect.
Now, let us observe the given diagram, we can see that both processes II and IV are depicted as a straight line.Therefore, both processes II and IV are isothermal.
During process II, the volume of the gas is increasing and temperature remains constant so it is an isothermal expansion. Hence, from 1st law of thermodynamics, we can deduce that,
$[Q = \Delta U + W]$
Here, $[Q]$ is net heat transfer in the system, $[\Delta U]$ is a change in internal energy of the system and $[W]$ is the total work done by the system.
Here, $[\Delta U = 0]$, $[W > 0]$
Therefore, $[Q > 0]$, hence in process II heat gets absorbed. So, option B is correct.
Again, process IV is isothermal compression, as the volume of gas is decreasing at constant temperature during the process. Hence, by 1st law of thermodynamics,
$[W < 0]$ and $[\Delta U = 0]$
Therefore the heat is released in this process as $[Q < 0]$. Hence, option C is also correct.
In an isobaric process, the pressure of the system does not change and temperature will be directly proportional to volume.
$[\therefore T\alpha V]$
In other words, if processes I and II would have been isobaric, then the Volume-Temperature graph should be of straight line. But, it is not true. Hence, process I and II are not isobaric.Hence, option D is correct.
Therefore, the correct options are options B, C and D.
Note:According to the first law of thermodynamics, the change in internal energy of a system is the same as that of the difference between the net heat transfer in the system and net work done by the system.
Mathematically, it can be expressed as,
$[\Delta U = Q - W]$
Here, $[Q]$ is net heat transfer in the system, $[\Delta U]$ is a change in internal energy of the system and $[W]$ is the total work done by the system.
If the value of Q is positive, then energy is added to the system and if W is positive the energy will be taken from the system by work.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




