Question

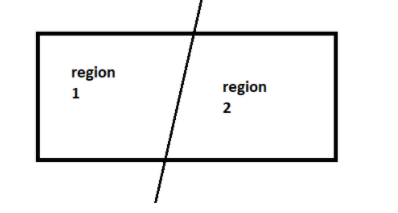
One line forms two regions in a plane. Similarly, two lines in a plane can form a maximum of four regions. These are shown in the figures.

What is the maximum number of regions that can be formed by 4 lines in a plane? Lines need not be concurrent.
A.7
B.8
C.10
D.11

Answer 1

Hint: At first we have given that One line forms two regions in a plane and two lines in a plane can form a maximum of four regions, similarly, we’ll find for the maximum number of regions for three lines.
From there we’ll get a particular type of series to easily determine the maximum regions made by four lines.

Complete step-by-step answer:
Given data: One line forms two regions in a plane
Two lines in a plane can form a maximum of four regions
Let's say that \[f\left( n \right)\] is the function resulting in the maximum regions that can be formed in a plane when n lines are there.
Now we know that one line forms 2 regions in a plane i.e.

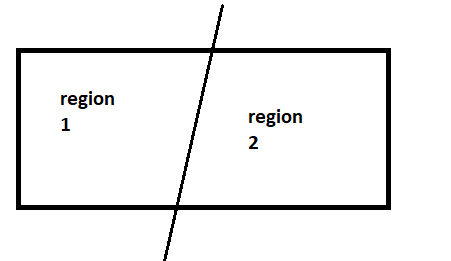
Therefore, $f(1) = 2$
Similarly, it is given that two lines in a plane can form a maximum of four regions

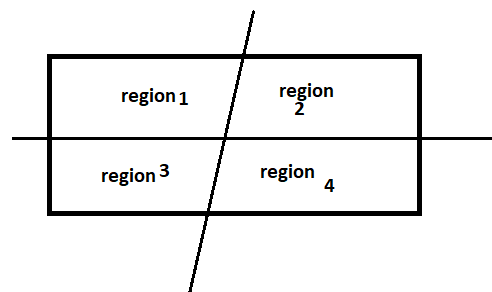
Therefore, $f(2) = 4$
Similarly, we can check for three lines

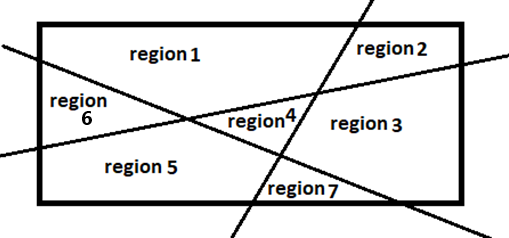
Therefore, three lines in a plane can form a maximum of seven regions
Therefore, $f(3) = 7$
From the value of \[f\left( 1 \right),{\text{ }}f\left( 2 \right),\]and \[f\left( 3 \right)\] we can conclude that as the ${n^{th}}$ is include the maximum region increases by ‘n’
That is \[f(3) = f(2) + 3\]
 \[ \Rightarrow f(3) = 4 + 3 = 7\]
Therefore, $f(4) = f(3) + 4$
On substituting the value of \[f\left( 3 \right)\] we get,
 $ \Rightarrow f(4) = 7 + 4$
 $\therefore f(4) = 11$
Therefore the required number of regions is 11.
Option(D) is correct.

Note: We can also proof the above solution as we found that
 $f(1) = 2$ , $f(2) = 4$ and $f(3) = 7$
We can say that the no lines include we have one area as a whole
i.e. $f(0) = 1$
Now $f(1) - f(0) = 1$
 $f(2) - f(1) = 2$
 $f(3) - f(2) = 3$
.
.
.
 $f(n) - f(n - 1) = n$
Adding all the above equations
 $ \Rightarrow f(n) - f(0) = 1 + 2 + 3 + 4........ + n$
Now we know that sum of first n natural numbers is given by $\dfrac{{n(n + 1)}}{2}$
 $ \Rightarrow f(n) - 1 = \dfrac{{n(n + 1)}}{2}$
Adding 1 on both sides
 $ \Rightarrow f(n) = \dfrac{{n(n + 1)}}{2} + 1$
Now substituting $n = 4$
 $ \Rightarrow f(4) = \dfrac{{4(5)}}{2} + 1$
 $ = 10 + 1$
 $ = 11$, which gives a similar answer as the above solution.