Question

One end of the string of length L and cross-sectional area A is fixed to a support and the other end is fixed to a bob of mass m. The bob is revolved in a horizontal circle of radius r with an angular velocity ω such that the string makes an angle θ with the vertical. The stress in the string is
\[\begin{align}
  & \text{A}\text{. }\dfrac{mg}{A} \\
 & \text{B}\text{. }\dfrac{mg}{A}\left( 1-\dfrac{r}{L} \right) \\
 & \text{C}\text{. }\dfrac{mg}{A}\left( 1+\dfrac{r}{L} \right) \\
 & \text{D}\text{. none of these} \\
\end{align}\]

Answer 1

Hint: We have given a set-up in which a string one end of string is fixed to a support and on the other end a bob of mass m is suspended and it is moving in a horizontal circle or having a circular motion. We have to find stress in the string. Stress is given as a ratio of tension T and cross sectional area A. By balancing the forces we can find T and hence stress.
Formula used:
\[\begin{align}
  & \text{Stress=}\dfrac{T}{A} \\
 & \cos \theta =\dfrac{\text{height}}{\text{hypotenuse}} \\
\end{align}\]

Complete answer:
Let us first draw a diagram for the given question.

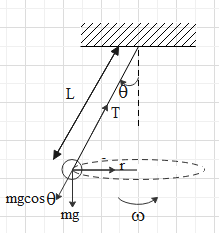
In the above diagram T is the tension in the string, mg is the gravitational pull due to the mass m of the bob and L is the length of the string. The string makes angle θ with the vertical plane. Also the bob is revolving in a horizontal plane of radius r and with angular velocity ω.
Here we have to find the stress and stress in the string is the tension per cross-sectional area and it is given as
\[\text{Stress=}\dfrac{T}{A}\]
Now cross sectional area of the string is given as A and by seeing the diagram and balancing the forces the tension in the string will be equal to the cosine component of the gravitational pull and can be written as
\[T=mg\cos \theta \]
Substituting this value of T in the above formula for stress we get
\[\text{Stress=}\dfrac{mg\cos \theta }{A}\text{ }........\text{(i)}\]
We can find the value of θ by considering a triangle from the above diagram which can be shown as

Here h is the height, L is hypotenuse and r is the base, now formula for cos θ is
\[\cos \theta =\dfrac{\text{height}}{\text{hypotenuse}}\]
Now height for a right angle triangle is given as
\[\begin{align}
  & \text{height=}\sqrt{{{\left( \text{hypotenuse} \right)}^{2}}-{{\left( \text{base} \right)}^{2}}} \\
 & \Rightarrow h=\sqrt{{{L}^{2}}-{{r}^{2}}} \\
\end{align}\]
Hence cos θ will be given as
\[\begin{align}
  & \cos \theta =\dfrac{\sqrt{{{L}^{2}}-{{r}^{2}}}}{L} \\
 & \Rightarrow \cos \theta =\sqrt{\dfrac{{{L}^{2}}-{{r}^{2}}}{{{L}^{2}}}} \\
 & \Rightarrow \cos \theta =\sqrt{1-\dfrac{{{r}^{2}}}{{{L}^{2}}}} \\
\end{align}\]
Now we can expand the right hand term from binomial expansion and write it as
\[\cos \theta =\left( 1-\dfrac{r}{L} \right)\]
Substituting this value of cos θ in the equation (i), we get
 \[\text{Stress=}\dfrac{mg}{A}\left( 1-\dfrac{r}{L} \right)\]

Hence option B is the correct answer.

Note:
The above answer is an approximate answer as in binomial expansion the terms with higher power are neglected. Also there will be centripetal force acting towards the center of the horizontal plane, it is not labelled to avoid confusion. In case the bob is at rest then the tension in the string will be equal to the downward gravitational pull.