Question

One angle of a Pentagon is ${{140}^{\circ }}$. If the remaining angles are in the ratio of 1:2:3:4. What is the size of the largest angle?

Answer 1

Hint: We start solving the problem by assuming the variables for the remaining angles present in the pentagon. We then find the sum of the angles present in the pentagon by recalling the fact that the sum of the angles in a polygon of ‘n’ sides is $\left( n-2 \right)\times {{180}^{\circ }}$. We then add the assumed angles and the given angle and equate it to the obtained sum. We then make the necessary calculations to find the sizes of all angles in the pentagon. We then check what is the highest size of the angles obtained to get the required value.

Complete step by step answer:
According to the problem, we are given that one angle of a Pentagon is ${{140}^{\circ }}$. We need to find the size of the largest angle if the remaining angles are in the ratio of 1:2:3:4.
Let us assume the remaining angles be $x$, $2x$, $3x$ and $4x$.
Let us draw the figure representing the given information.

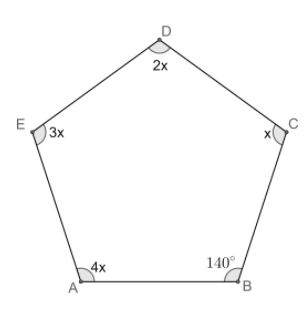
We know that the sum of the angles in a polygon of ‘n’ sides is $\left( n-2 \right)\times {{180}^{\circ }}$.
Now, let us find the sum of the angles in the Pentagon. So, the sum of angles in Pentagon is $\left( 5-2 \right)\times {{180}^{\circ }}=3\times {{180}^{\circ }}={{540}^{\circ }}$.
Now, we have $x+2x+3x+4x+{{140}^{\circ }}={{540}^{\circ }}$.
$\Rightarrow 10x={{400}^{\circ }}$.
$\Rightarrow x={{40}^{\circ }}$.
Let us find the size of the remaining angles using the value of $x$.
Now, we have $2x=2\times {{40}^{\circ }}={{80}^{\circ }}$.
Also, $3x=3\times {{40}^{\circ }}={{120}^{\circ }}$ and $4x=4\times {{40}^{\circ }}={{160}^{\circ }}$.
We can see that the size of the largest angle is ${{160}^{\circ }}$.

∴ The size of the largest angle is ${{160}^{\circ }}$.

Note: Here we have assumed that the polygon is closed convex one not the other. We should assume the variables appropriately in order to avoid confusion and reduce calculation time. Whenever we get the problem involving the polygons, we first try to recall the number of sides and angles of present in it so that we can get the correct answer. Similarly, we can expect the problems to find the sum of the external angles present in the Pentagon given in the problem.