Question

On a square handkerchief, nine circular designs each of radius 7cm are cut. Find the area of the remaining portion of the handkerchief.

Answer 1

Hint: Determine the length of a side of the square. Then use the formula for the area of a square $={{a}^{2}}$ and the area of a circle $=\pi {{r}^{2}}$. Use the fact that the remaining area is the area of all the circles subtracted from the area of the square.

Complete step-by-step solution -

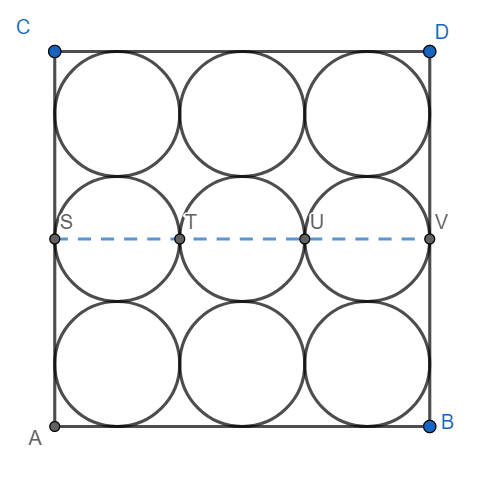
We have the length of a side of the square = SV = ST +TU +UV.
Since ST, TU and UV are the diameters of the circles; we have ST = TU = UV = 14.
Hence the length of a side of the square is 14+14+14=42
Area of the square $={{a}^{2}}={{42}^{2}}=1764$ square centimetres.
Also area of a circle $=\pi {{r}^{2}}=\dfrac{22}{7}\times {{7}^{2}}=154$square centimetres.
Hence the area of the nine circles is $=9\times 154=1386$ square centimetres
Hence we have the remaining area of the handkerchief =area of the square – area of the nine circles = 1764 – 1386 =378 square centimetres.

Note: Alternative solution
We can enclose each circle in a square of 1cm and find the area of the remaining portion as shown

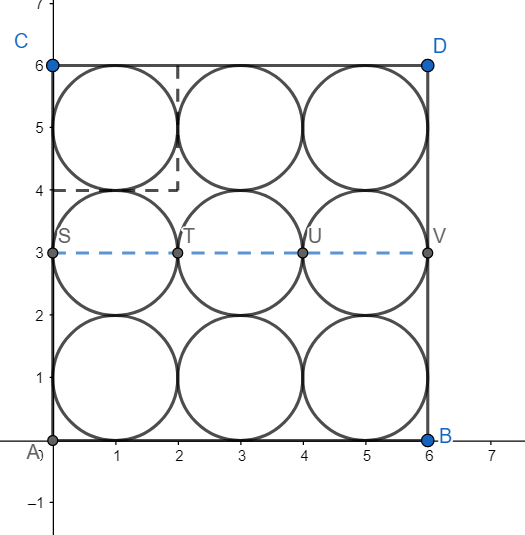
Area of the remaining portion $={{\left( 14 \right)}^{2}}-\dfrac{22}{7}{{\left( 7 \right)}^{2}}=196-154=42$
Hence the total area of the remaining portion $=9\times 42=378$