Question

On a map drawn to a scale of \[1:50,000\], a rectangular plot of land \[ABCD\] has the following dimensions.\[AB=6cm; BC=8cm\] and all the angles are right angles. Find the actual length of the diagonal distance \[AC\] of the plot in km.

Answer 1

Hint: Since the given figure is a rectangle and all the angles are right angles we use the Pythagoras theorem to find the diagonal length. Pythagoras theorem states that the square of the hypotenuse is equal to the sum of squares of the other two sides of the triangle that is for a triangle shown below the Pythagoras theorem can be applied as follows

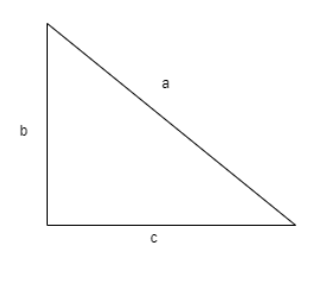
Applying Pythagoras theorem for above figure, \[{{a}^{2}}={{b}^{2}}+{{c}^{2}}\].
After getting the diagonal length we then convert it into the map by multiplying with 50,000 as one unit is equal to 50,000 on the map.

Complete step-by-step solution
Let us assume that the given rectangle will look like

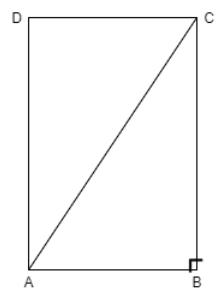
We are given that \[AB=6cm; BC=8cm\].
Pythagoras theorem states that the square of the hypotenuse is equal to the sum of squares of the other two sides of the triangle hat is for a triangle shown below the Pythagoras theorem can be applied as follows
 

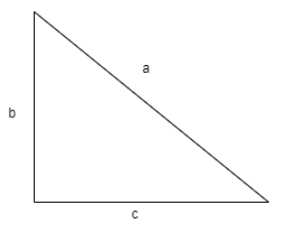
Applying Pythagoras theorem for above figure, \[{{a}^{2}}={{b}^{2}}+{{c}^{2}}\].
Now, let us apply Pythagoras theorem to the triangle \[\Delta ABC\] we get
\[\Rightarrow A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}\]
Now by substituting \[AB=6cm;BC=8cm\] in above equation we will get
\[\begin{align}
  & \Rightarrow A{{C}^{2}}={{\left( 6cm \right)}^{2}}+{{\left( 8cm \right)}^{2}} \\
 & \Rightarrow A{{C}^{2}}=\left( 36+64 \right)c{{m}^{2}} \\
 & \Rightarrow A{{C}^{2}}=100c{{m}^{2}} \\
\end{align}\]
Now, by applying square root on both sides we get
\[\begin{align}
  & \Rightarrow AC=\sqrt{100c{{m}^{2}}} \\
 & \Rightarrow AC=10cm \\
\end{align}\]
Here, we got the original length of diagonal as 10cm.
Let us convert this length to map dimensions.
We are given that the scale in the map is \[1:50,000\] we need to multiply the original length by 50,000 to get the length in the map scale.
By multiplying with 50,000 to length of diagonal we get
\[\begin{align}
  & \Rightarrow AC=\left( 10cm \right)\times 50,000 \\
 & \Rightarrow AC=5,00,000cm \\
\end{align}\]
We know that \[1km=1,00,000cm\] or \[1cm=\dfrac{1}{1,00,000}km\].
By applying this to AC we get
\[\begin{align}
  & \Rightarrow AC=\left( 5,00,000 \right)\left( \dfrac{1}{1,00,000} \right)km \\
 & \Rightarrow AC=5km \\
\end{align}\]
Therefore the length of diagonal in the map is 5km.

Note: Students may make mistakes in converting the original length to map dimensions that are instead of multiplying with 50,000 due to confusion they may divide by 50,000. In the question, \[1:50,000\] means one unit of original length is equal to 50,000 units in map dimensions. So, we need to multiply with 50,000 not divide with 50,000.