Question

Obtain the volume of the rectangular box with the following length, breadth and height respectively:
$5a,3{{a}^{2}},7{{a}^{4}}$.
(a) $102{{a}^{7}}$
(b) $105{{a}^{7}}$
(c) $192{{a}^{7}}$
(d) $606{{a}^{7}}$

Answer 1

Hint: We will draw a rough diagram of the box and label the length, breadth, and height of the box. We will use the formula for the volume of a cuboid to find the volume of the rectangular box. The volume of the cuboid is given by $V=l\times b\times h$ where $l$ is the length, $b$ is the breadth and $h$ is the height of the box. We will also use the law of indices which states that ${{a}^{m}}\times {{a}^{n}}={{a}^{m+n}}$.

Complete step by step answer:
Let u draw a diagram that represents the rectangular box. The figure looks like the following,

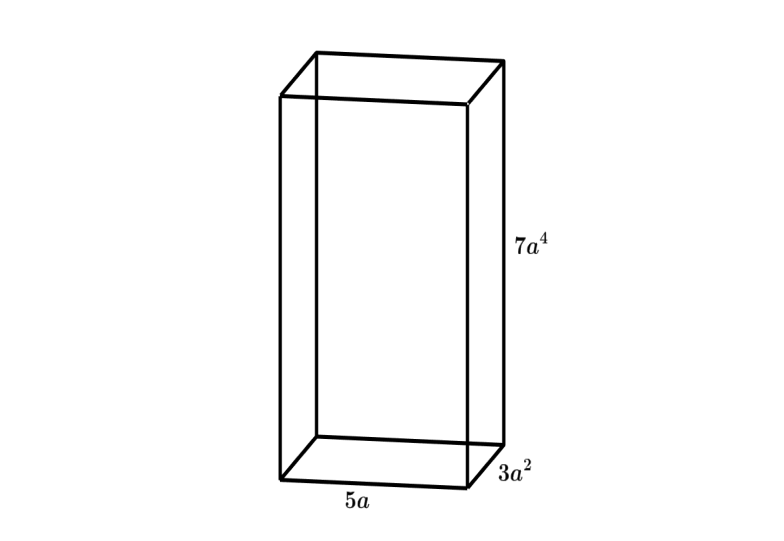
A rectangular box has the shape of a cuboid. Therefore, to find the volume of the rectangular box, we will use the formula for the volume of cuboid. The volume of cuboid is given by $V=l\times b\times h$ where $l$ is the length, $b$ is the breadth and $h$ is the height. We are given that $l=5a$, $b=3{{a}^{2}}$ and $h=7{{a}^{4}}$. Substituting these values in the formula for the volume of cuboid we get the following,
\[\begin{align}
  & \text{volume of box}=5a\times 3{{a}^{2}}\times 7{{a}^{4}} \\
 & \therefore \text{volume of box}=\left( 5\times 3\times 7 \right)\times \left( a\times {{a}^{2}}\times {{a}^{4}} \right) \\
\end{align}\]
Here, we used the commutative property of multiplication. This property states that the order in which the numbers are multiplied does not change the product. So, we have the following,
\[\text{volume of box}=105\times \left( a\times {{a}^{2}}\times {{a}^{4}} \right)\]
Now, we know the law of indices which states that ${{a}^{m}}\times {{a}^{n}}={{a}^{m+n}}$. Therefore, according to this law, we have
$\begin{align}
  & a\times {{a}^{2}}\times {{a}^{4}}={{a}^{1+2+4}} \\
 & \therefore a\times {{a}^{2}}\times {{a}^{4}}={{a}^{7}} \\
\end{align}$
Substituting this in the expression above, we get the following,
\[\text{volume of box}=105{{a}^{7}}\]
Hence, the volume of the rectangular box is $105{{a}^{7}}$. The correct option is (b).
Note:
 It is important to understand the three-dimensional shape using the description given. It is important to know the standard three-dimensional shapes and the formulae for their volumes and surface areas. We should be familiar with the laws of indices as they are helpful in calculations. A diagram representing the shape and its measurements is always helpful.