Question

When observed from top of a tower, the angle of depression of two houses A and B in the eastern and western directions is ${30^ \circ }$ and ${60^ \circ }$ respectively, then
A. House A is nearer to the tower than house B.
B. House B is nearer to the tower than house A
C. House A and B are equidistant from the tower
D. None of these

Answer 1

Hint: We will first draw a figure related to the information given to us and see two triangles in it in which we will use trigonometric values to the assumed height of the tower and distance. By equating those, we will have our answer.

Complete step-by-step answer:
Let us first draw the image as required. Let MN be the tower and A and B be the two houses and their angle of depression are as mentioned below in the figure. Let h units be the height of the tower. Let the distance of house ‘A’ and ‘B’ from tower MN be x units and y units respectively.
It will turn out to be as follows:-
               

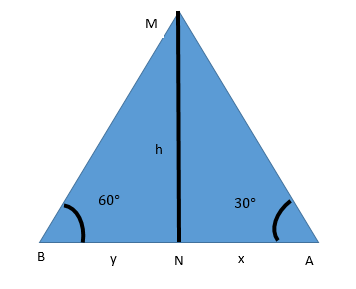
We know that $\tan \theta = \dfrac{{Perpendicular}}{{Base}}$ …….(1)
Now, first of all consider $\vartriangle MNB$. We have one angle 60 degrees. We will apply the formula in (1) on this angle. We will get:-
$\tan {60^ \circ } = \dfrac{{MN}}{{NB}}$
Now putting in the values, we will get:-
$\sqrt 3 = \dfrac{h}{y}$
We can rewrite it as:-
$h = \sqrt 3 y$ ……………(2)
Now, consider $\vartriangle MNA$. We have one angle 30 degrees. We will apply the formula in (1) on this angle. We will get:-
$\tan {30^ \circ } = \dfrac{{MN}}{{NA}}$
Now putting in the values, we will get:-
$\dfrac{1}{{\sqrt 3 }} = \dfrac{h}{x}$
We can rewrite it as:-
$h = \dfrac{x}{{\sqrt 3 }}$
$ \Rightarrow h = \dfrac{x}{{\sqrt 3 }} \times \dfrac{{\sqrt 3 }}{{\sqrt 3 }} = \dfrac{{\sqrt 3 x}}{3}$ ……………(3)
Equating (2) and (3), we will get:-
$ \Rightarrow \sqrt 3 y = \dfrac{{\sqrt 3 x}}{3}$
Cross multiplying to get the following expression:-
$ \Rightarrow 3\sqrt 3 y = \sqrt 3 x$
Taking $\sqrt 3 $ common from both sides and cutting it off, we will get:-
$ \Rightarrow 3y = x$
Clearly, we can see that x is greater than y.
Hence, House B is nearer to the tower than house A.

So, the correct answer is “Option B”.

Note: The students must remember to form the figure before starting off with the question because forming an image would help you imagine and think better whereas not forming it can create chaos and mistakes.
As while equating, we cut off the common factor of $\sqrt 3 $. We cannot do the same with a variable factor which can take the value of 0 as well. We can only cut off which are definitely never equal to 0.