Question

O is the center of a circle with diameter 30 cm. P is a point outside the circle and PA is tangent of the circle, then find: (i) The length of tangent PA; if OP = 39 cm, (ii) The distance between O and P, if the length of the tangent PA is 20 cm.
A. (i) 39 cm, (ii) 27 cm
B. (i) 36 cm, (ii) 25 cm
C. (i) 27 cm, (ii) 39 cm
D. (i) 25 cm, (ii) 36 cm

Answer 1

Hint: A circle with center O and a tangent PA is given. By looking at the question it is evident that the radius of the circle can be found out using the given diameter. Both the two parts of the question are easy to solve if you know that the angle made by the tangent drawn to the circle i.e, PA with the line joining O and P is 90°.Then by using Pythagora's theorem we will obtain the required solution.

Complete step-by-step answer:
Let us first convert the given question into a diagram

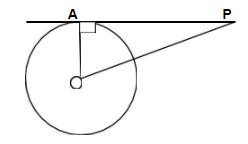
Given that diameter = 30cm
As we know radius =\[\dfrac{diameter}{2}\]= 15cm
Let the radius of the circle be denoted by r i.e r= 15cm
(i) It is given that OP = 39cm
In the ∆OPA as we know that \[\angle OAP={{90}^{\circ }}\]
We now have a right angled triangle with sides
OA(radius) = 15cm, OP = 39cm and PA
As we know Pythagoras theorem can be used in a right angled triangle
It implies that \[O{{A}^{2}}+P{{A}^{2}}=O{{P}^{2}}\]
Substituting the given values we get
\[\begin{align}
  & {{\left( 15 \right)}^{2}}+P{{A}^{2}}={{\left( 39 \right)}^{2}} \\
 & P{{A}^{2}}=1521-225 \\
 & P{{A}^{2}}=1296 \\
 & PA=\sqrt{1296}=36cm \\
\end{align}\]
AP = 36cm
(ii) Given PA = 20cm
We have AP = 20cm, OA = 15cm and PA
Again by using Pythagoras theorem
 \[O{{A}^{2}}+P{{A}^{2}}=O{{P}^{2}}\]
Substituting the given values we get
\[\begin{align}
  & {{\left( 15 \right)}^{2}}+{{\left( 20 \right)}^{2}}=O{{P}^{2}} \\
 & O{{P}^{2}}=225+400=625 \\
 & OP=\sqrt{625}=25cm \\
\end{align}\]
OP = 25cm

So, the correct answer is “Option B”.

Note: The value given in the question is of the diameter of the circle, so students shouldn’t confuse it with the radius. As there are two sub questions in a single question values should be noted down with at most precision. If the question is given as just a MCQ question then just by solving the first part of the question we would know that the correct answer is option B.