Question

What is the nature of the graph drawn between mass and acceleration for a constant force? Does the graph pass through origin?

Answer 1

Hint: To answer this question, we need to use Newton's second law of motion to write the relation between the force, the mass, and the acceleration. Then for a constant force we will get an equation between mass and acceleration, from which we can predict the nature of the graph between them.

Formula used: The formula used to solve this question is given by
 $ F = ma $, here $ F $ is the force acting on an object of mass $ m $ which is having an acceleration of $ a $.

Complete step by step answer
We know from Newton's second law of motion that the force applied on a body is directly proportional to the rate of change of momentum of the body. If the mass doesn’t change during the motion of the body, then this can be mathematically expressed as
 $ F = ma $
According to the question, the force is constant. Therefore, substituting $ F = c $ we get
 $ ma = c $
Now, if we plot the mass on the x-axis and the acceleration on the y-axis, then we can substitute $ m = x $, and $ a = y $ in the above equation to obtain
 $ xy = c $
We know that this is the equation of a rectangular hyperbola. So the graph between mass and acceleration can be represented as

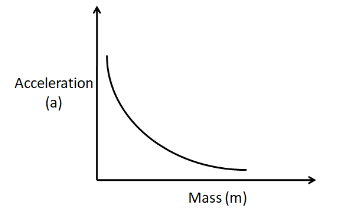
As we can see that the graph approaches the x and the y axis. It will approach both of the axes till infinity. So neither the mass, nor the acceleration can become zero. Hence, the graph cannot pass through the origin.

Note
We may argue what would happen if the constant force becomes zero. In that case, the acceleration will become zero, and the graph will be the x-axis itself. But in that case too, the graph will not be defined at the origin, as there is no concept of mass being zero. Hence, the graph between mass and acceleration can never pass through the origin.