Question

Name the type of triangle PQR formed by the points \[P(-\sqrt{2},\sqrt{2})\], \[Q(-\sqrt{2},-\sqrt{2})\] and \[R(-\sqrt{6},\sqrt{6})\].

Answer 1

Hint: Find the distance between the PQ, QR and RP using the distance formula. Then check, if all the distances are same then it is equilateral triangle, or if two distances are same then it is isosceles triangle else scalene triangle. The distance formula, \[d=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}\]. Here \[({{x}_{1}},{{y}_{1}})\]and \[({{x}_{2}},{{y}_{2}})\] are two points between which the distance (d) is to be found.

Complete step-by-step answer:
In the question, we have to find the type of triangle PQR formed by the points \[P(-\sqrt{2},\sqrt{2})\], \[Q(-\sqrt{2},-\sqrt{2})\] and \[R(-\sqrt{6},\sqrt{6})\].
So, we will use the distance formula here and will find the length of each line that joins points PQ, QR and PR.
Now, the distance formula between the two points is given as follows.

Now, distance (d) between points \[({{x}_{1}},{{y}_{1}})\] and \[({{x}_{2}},{{y}_{2}})\]
is found using the formula: \[d=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}\]
So now, the distance between \[P(-\sqrt{2},\sqrt{2})\] and \[Q(-\sqrt{2},-\sqrt{2})\] is given by:
\[\begin{align}
  & \Rightarrow PQ=\sqrt{{{\left( -\sqrt{2}-(-\sqrt{2}) \right)}^{2}}+{{\left( -\sqrt{2}-(\sqrt{2}) \right)}^{2}}} \\
 & \because {{x}_{2}}=-\sqrt{2}\,,\,\,{{x}_{1}}=-\sqrt{2},\,\,{{y}_{2}}=-\sqrt{2}\,,\,\,{{y}_{1}}=\sqrt{2} \\
 & \Rightarrow PQ=\sqrt{{{0}^{2}}+{{\left( -2\sqrt{2} \right)}^{2}}} \\
 & \Rightarrow PQ=2\sqrt{2} \\
\end{align}\]
Next, the distance between \[Q(-\sqrt{2},-\sqrt{2})\] and \[R(-\sqrt{6},\sqrt{6})\], is given by:
\[\begin{align}
  & \Rightarrow QR=\sqrt{{{\left( -\sqrt{6}-(-\sqrt{2}) \right)}^{2}}+{{\left( \sqrt{6}-(-\sqrt{2}) \right)}^{2}}} \\
 & \because {{x}_{2}}=-\sqrt{6}\,,\,\,{{x}_{1}}=-\sqrt{2},\,\,{{y}_{2}}=\sqrt{6}\,,\,\,{{y}_{1}}=-\sqrt{2} \\
 & \Rightarrow QR=\sqrt{{{\left( -\sqrt{6}+\sqrt{2} \right)}^{2}}+{{\left( \sqrt{6}+\sqrt{2}) \right)}^{2}}} \\
 & \Rightarrow QR=\sqrt{\left( 6+2-2\sqrt{12} \right)+\left( 6+2+2\sqrt{12} \right)} \\
 & \Rightarrow QR=4 \\
\end{align}\]

Next, we will find the distance between \[R(-\sqrt{6},\sqrt{6})\] and \[P(-\sqrt{2},\sqrt{2})\], which is given by:
\[\begin{align}
  & \Rightarrow RP=\sqrt{{{\left( -\sqrt{2}-(-\sqrt{6}) \right)}^{2}}+{{\left( \sqrt{2}-(\sqrt{6}) \right)}^{2}}} \\
 & \because {{x}_{2}}=-\sqrt{2}\,,\,\,{{x}_{1}}=-\sqrt{6},\,\,{{y}_{2}}=\sqrt{2}\,,\,\,{{y}_{1}}=\sqrt{6} \\
 & \Rightarrow RP=\sqrt{{{\left( -\sqrt{2}+\sqrt{6} \right)}^{2}}+{{\left( \sqrt{2}-\sqrt{6} \right)}^{2}}} \\
 & \Rightarrow QR=\sqrt{\left( 2+6-2\sqrt{12} \right)+\left( 2+6-2\sqrt{12} \right)} \\
 & \Rightarrow QR=\left( 8-2\sqrt{12} \right) \\
\end{align}\]
So, here we can see that all three distances points PQ, QR and PR are unequal. Hence, this is a scalene triangle with no two sides lengths equal.

Note: The alternative method to solve this problem is graphically. We will first plot all the points and then draw the line joining them to form a triangle. So, the diagram will look as follows:

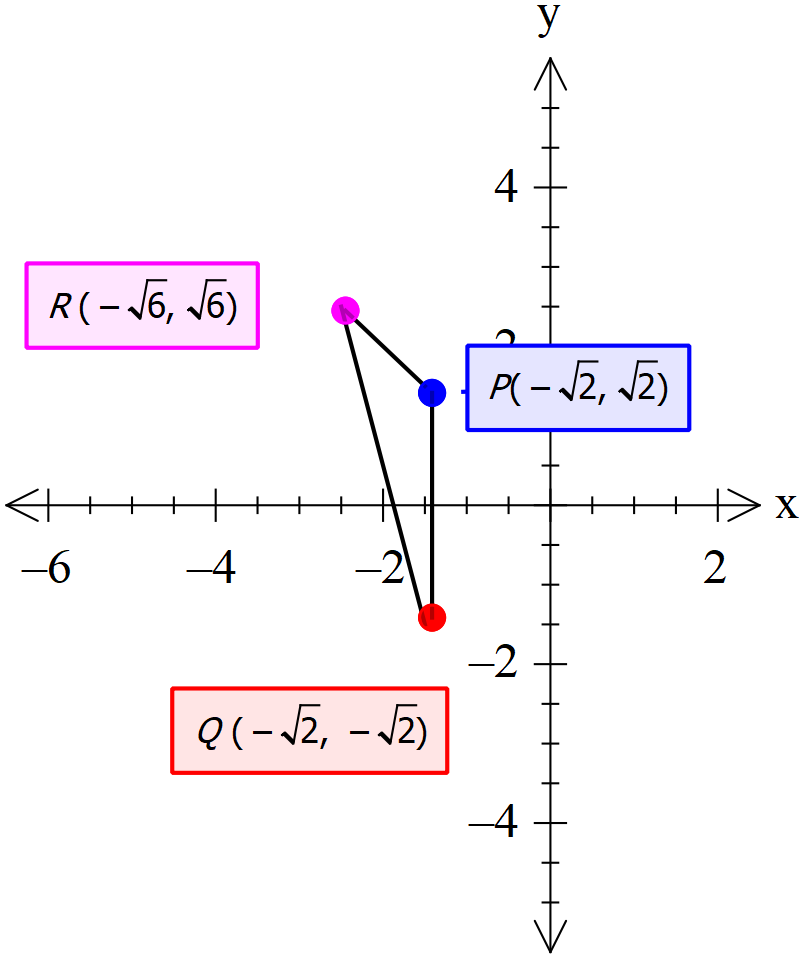
Now, here all the three sides are unequal as can be seen graphically. So, it is a scalene triangle with all three sides of unequal lengths.