Question

Name the quadrilateral which has both line and rotational symmetry of order more than 1.

Answer 1

Hint: A quadrilateral is a polygon which has four sides. According to the question, we have to draw such a quadrilateral that has both the line and rotational symmetry of order more than 1. This means that when the quadrilateral is rotated in a full circle, there should be an angle less than \[{{360}^{\circ }}\]at which the figure resembles the unrotated figure. Also, the question demands that there should be at least two lines with respect to which the quadrilateral drawn is symmetric. So, let us see, what kind of quadrilateral satisfies both the above conditions.

Complete step-by-step answer:
The quadrilateral which satisfies both the conditions given in question is a rectangle. Let us see how it satisfies those conditions.

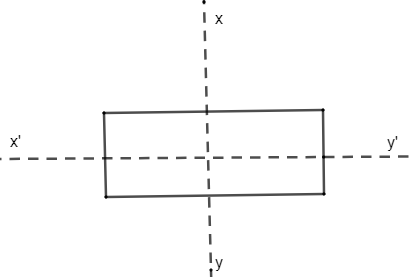
From the figure drawn above, we can see clearly two lines of symmetry which are perpendicular to each other. Thus one of the conditions is leaving fulfilled by the rectangle. Now, let us check the condition of rotational symmetry. So to check this condition, start rotating the figure. We will notice that when the figure is rotated through \[{{180}^{\circ }}\], it appears to be the same as the unrotated figure. Thus we can say that a rectangle exhibits rotational symmetry of order 2.
Thus, a rectangle is a quadrilateral which has both the line and rotational symmetry of order more than 1.

Note: Instead of a rectangle, the answer of the above question could have been a square. A square has 4 lines of symmetry and order of rotational symmetry equal to 4. Thus a square satisfies both the conditions given in the question.