Question

Name any two figures that have both line symmetry and rotational symmetry.

Answer 1

Hint: Rotational symmetry is the property a shape has when it looks the same after some rotation by a partial turn. Line symmetry is a type of symmetry with respect to reflection. Thus, in the question, we have to basically draw those figures which when rotated through an angle (less than\[{{360}^{o}}\]) looks exactly the same as the figure in original form and they should also have symmetry with respect to the axis passing through them. So, let us start the solution of the above question.

Complete step-by-step answer:
So, now we will start drawing the figures which have both rotational and line symmetry. So our first figure is an equilateral triangle: -

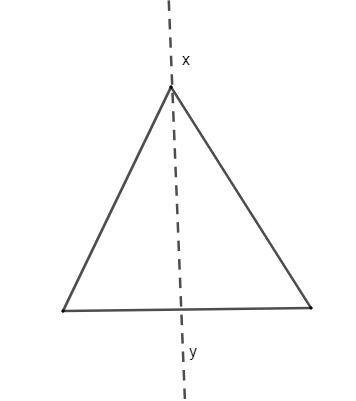
We can see that, in the above triangle, the figure is symmetry with respect to the axis line x-y. So, the x-y line acts as a mirror for one portion of the triangle. Therefore, we can say that an equilateral triangle has a line symmetry. Also when the figure is rotated through \[{{120}^{o}},{{240}^{o}},{{360}^{o}}\] it appears to be same as the original figure. So, it has rotational symmetric. Thus, we can say that an equilateral triangle has both line and rotational symmetry.
Our next figure is a rectangle: -

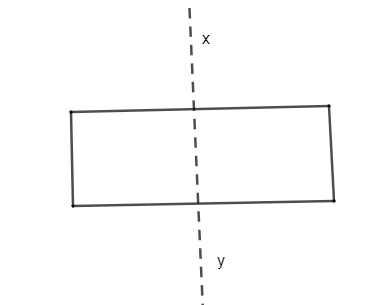
We can see that in the above rectangle the figure is symmetric with respect to the axis line x-y. SO, the x-y line acts as a mirror for one portion of the rectangle. Therefore, we can say that a rectangle has a line symmetry. Also, when the figure is rotated through \[{{180}^{o}}\] and \[{{360}^{o}}\], it appears to be same as the original figure. So, it has rotational symmetry. Thus, we can say that a rectangle has both line and rotational symmetry.
So, a triangle and a rectangle has both line and rotational symmetry.

Note: Instead of a triangle and a rectangle, we can have any regular polygon because regular polygons of any number of sides have both line symmetry and rotational symmetry.