Question

Mulf A, B, and C are three mutually exclusive events, the probability of their union is equal to__________
A. $P(A)P(B)P(C)$
B. $P(A) + P(B) + P(C) - P(ABC)$
C. $P(A) + P(B) + P(C)$
D. $P(A)P(B) + P(C)P(A) + P(B)P(C)$

Answer 1

Hint: According to the question given in the question we have to determine the probability of their union when mulf A, B, and C are three mutually exclusive events. So, first of all we have to understand about the mutually exclusive event which is as explained below:
According to probability theory, two events are said to be mutually exclusive if they can’t occur at the same time or simultaneously and we can also called the mutually exclusive events as the disjoint event. If two or three events are considered as a disjoint event, then the probability of both events occurring at the same time will be zero.
If A, B and C are three mutually exclusive events, then the probability of disjoint of events A, B and C can be represented as:
Probability of disjoint or mutually exclusive event $P(AandB) = 0$
Probability of disjoint or mutually exclusive event $P(AorB) = P(A) + P(B)$
Now, we have to determine the diagram for the all three mutually exclusive events and with the help of diagrams we can determine the probability of their union.

Complete step-by-step solution:
Step 1: Now, if A, B and C are three mutually exclusive events, then the probability of disjoint of events A, B and C can be represented as mentioned in the solution hint if two or three events are considered as a disjoint event, then the probability of both events occurring at the same time will be zero so, first of all we have to draw the diagram.

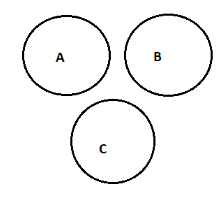
Step 2: Now, as from the diagram as we obtained in the solution step 1 we can see that there is no any common point between them or we can say that there is no intersection in between all the three mutually exclusive events which are A, B, and C.
Step 3: Now, as from the solution step 2 according to the diagram we can see that there are no intersections between the points. Hence,
$ \Rightarrow P(A \cup B \cup C) = P(A) + P(B) + P(C)$
Final solution: Hence, we have determined the probability of all the three events A, B, and C union is equal to$P(A) + P(B) + P(C)$.

Therefore option (C) is correct.

Note: In probability the specific addition is valid when two or three events are mutually exclusive and it stated that the probability of either event occurring is the sum of the probability of each occurring event.
Two events are said to be mutually exclusive if they can’t occur at the same time or simultaneously and we can also called the mutually exclusive events as the disjoint event.