Question

What is the moment of inertia of a ring about a tangent to the circle of the ring?

Answer 1

Hint: Moment of inertia is the rotational analogue of mass for linear motion. The axis of rotation has to be specified with the moment of inertia. For point mass, the moment of inertia is mass times square of the perpendicular distance to the rotational axis. Moment of inertia of common objects is calculated by perpendicular and parallel axis theorems.

Formula used:
$\begin{align}
  & {{\text{I}}_{\text{New}}}={{\text{I}}_{\text{cm}}}+\text{m}{{\text{d}}^{\text{2}}} \\
 & {{\text{I}}_{\text{cm}}}=\text{m}{{\text{r}}^{\text{2}}} \\
\end{align}$

Complete step-by-step answer:
The moment of inertia of a ring about a tangent parallel to the diameter is guided by parallel axis theorem. It is applicable for bodies of any shape. The theorem states that the moment of inertia of a body about an axis is equal to the sum of its moment of inertia about a parallel axis passing through the centre of mass and the product of mass and square of the distance between two axes.
$\begin{align}
  & {{\text{I}}_{\text{New}}}={{\text{I}}_{\text{cm}}}+\text{m}{{\text{d}}^{\text{2}}} \\
 & {{\text{I}}_{\text{cm}}}=\text{m}{{\text{r}}^{\text{2}}} \\
\end{align}$

Here ${{\text{I}}_{\text{cm}}}$ is the moment of inertia along the centre of mass of the object. The new centre of mass is the sum of ${{\text{I}}_{\text{cm}}}$ and mass times distance of separation to the new axis. In the case of a moment of inertia of a ring about a tangent to the circle of the ring. Here M is the mass of the ring and R radius of the ring.

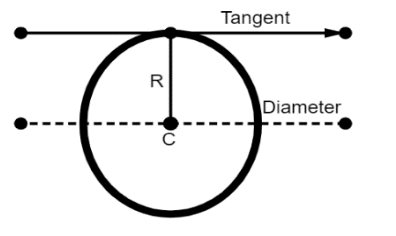
By applying parallel axis theorem, we can write as,
$\begin{align}
  & {{\text{I}}_{\text{cm}}}=\text{M}{{\text{R}}^{\text{2}}} \\
 & \text{m}{{\text{d}}^{\text{2}}}=\dfrac{\text{M}{{\text{R}}^{\text{2}}}}{2} \\
 & {{\text{I}}_{\text{New}}}\text{=M}{{\text{R}}^{\text{2}}}\text{ + }\dfrac{\text{M}{{\text{R}}^{\text{2}}}}{2}\text{ } \\
 & \\
\end{align}$
Therefore the moment of inertia of a ring along the tangent to the circle is,
 ${{\text{I}}_{\text{New}}}\text{=}\dfrac{\text{3M}{{\text{R}}^{\text{2}}}}{2}$
The moment of inertia of a ring about a tangent to the circle of the ring is ${{\text{I}}_{\text{New}}}\text{=}\dfrac{\text{3M}{{\text{R}}^{\text{2}}}}{2}$

Note: The moment of inertia of planar objects are guided by perpendicular axis theorem ${{\text{I}}_{\text{Z}}}\text{=}{{\text{I}}_{\text{X}}}\text{+ }{{\text{I}}_{\text{Y}}}$ (${{\text{I}}_{\text{X}}}\text{, }{{\text{I}}_{\text{Y}}}\text{, }{{\text{I}}_{\text{Z}}}$ are the moment of inertia along x, y, z-axis respectively). The moment of inertia of rigid bodies is guided by parallel axis theorem. Care should be taken in calculating the distance of separation from the centre of mass to the tangent placed.