Question

What is the moment of inertia of a disc about one of its diameters?

Answer 1

Hint: Moment of inertia of disk about its axis is known and we also know the theorem of the perpendicular axis. So first we have to find the moment of inertia of the disk for the axis and then for diameter. Here note that moment of inertia about diameter for the perfect disc is the same for all diameters.

Formula used:
1) For moment of inertia about axis: \[{{I}_{z}}=\dfrac{M{{R}^{2}}}{2}\]
2) For perpendicular axis theorem is: \[{{I}_{z}}={{I}_{x}}+{{I}_{y}}\]

Complete step-by-step answer:
Moment of inertia: As per Newton’s first law of motion every object will remain at rest or in a uniform motion till the external force is not applied because every object tries to remain in its state of motion which defines INERTIA.
Inertia has two types linear and angular. Here we use the angular inertia. A quantity that explains any object’s tendency to resist its angular motion is called the angular moment of inertia.

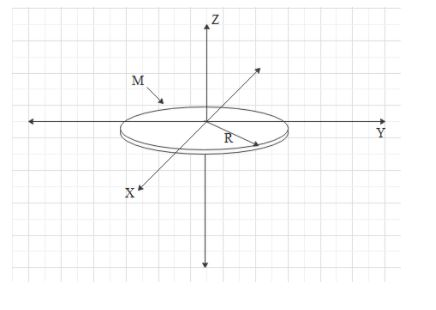
Here let’s assume the X, Y and Z axis of a disc. We have to find the moment of inertia about diameter or can say about the X-axis or Y-axis because the Z-axis is perpendicular to the disc which does not show diameter through it.
Let assume that the radius of the given disc is and the mass of the given disc is.

First of all, we have to find the moment of inertia about Z – axis, we can apply the formula which given above,
\[{{I}_{z}}=\dfrac{M{{R}^{2}}}{2}\]
Now, we have to find for the moment of inertia about diameter is let say \[{{I}_{x}}\] or \[{{I}_{y}}\] and both diameter is equal so moment of inertia about both diameter is also equal.
\[\therefore {{I}_{x}}={{I}_{y}}\]
Now the main part of the sum is to find the moment of inertia of a disc about its diameter. Here we can apply,
\[{{I}_{z}}={{I}_{x}}+{{I}_{y}}\]
But, \[{{I}_{z}}=\dfrac{M{{R}^{2}}}{2}\] and \[{{I}_{x}}={{I}_{y}}\]
\[\therefore \dfrac{M{{R}^{2}}}{2}=2{{I}_{x}}\]
\[\therefore {{I}_{x}}=\dfrac{M{{R}^{2}}}{2}\times \dfrac{1}{2}\]
\[\therefore {{I}_{x}}=\dfrac{M{{R}^{2}}}{4}\]
The moment of inertia of a disc about one of its diameters is \[{{I}_{x}}=\dfrac{M{{R}^{2}}}{4}\].

Additional Information: The moment of inertia of the solid cylinder about its axis is the same as the moment of inertia of the disc about its axis. Because the disc is a compressed solid cylinder or we can say that a solid cylinder has a very small height is called a disc.

Note:
1) In short the moment of inertia of a disc about its one of the diameters is equal to the one-fourth of its moment of inertia about its one of the axes.
2) Also, note that the moment of inertia of disc and ring is different because the disc has a solid volume but the ring has only a perimeter. The moment of inertia of the ring about its axis is \[M{{R}^{2}}\] and the moment of inertia of the disc is \[\dfrac{M{{R}^{2}}}{2}\].