Question

What is the minimum value of $F$ needed so that block begins to move upward on frictionless incline plane as shown

Answer 1

Hint: In the given question we have to find all the forces and the tension forces that work on the body $M$. Thus, we have to formulate a free body diagram here. Then by using the trigonometric ratios and Newton’s Law we will find the force $F$ that is needed to move the block upwards.

Complete step by step answer:

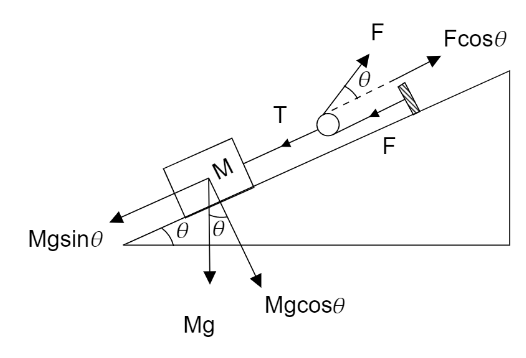
In the given figure, it is clear that the weight $Mg$ acts downward.By resolving the components of the weight $Mg$ we get the vertical component is $Mg\cos \theta $ and the horizontal component is $Mg\sin \theta $. The horizontal component $Mg\sin \theta $ is the force that balances the tension $T$ of the string.We can write,
$T = Mg\sin \theta - - - - - \left( 1 \right)$

Now, resolving the components of the force $F$ which is actually the tension in the string.
The horizontal component of the tension or force $F$ is $F\cos \theta $.Hence from the given diagram we get,
$T = F + F\cos \theta - - - - - \left( 2 \right)$
Comparing both the equations it is clear that,
$F + F\cos \theta = Mg\sin \theta $
Taking $F$ common from the left side of the equation we get,
$F\left( {1 + \cos \theta } \right) = Mg\sin \theta $

From the half angle formula of the trigonometry we get,
$F\left( {2{{\cos }^2}\dfrac{\theta }{2}} \right) = Mg\left( {2\sin \dfrac{\theta }{2}\cos \dfrac{\theta }{2}} \right)$
Dividing both sides by $2\cos \dfrac{\theta }{2}$ we get,
$F\left( {\cos \dfrac{\theta }{2}} \right) = Mg\left( {\sin \dfrac{\theta }{2}} \right)$
Arranging the equation we get,
$F = Mg\left( {\dfrac{{\sin \dfrac{\theta }{2}}}{{\cos \dfrac{\theta }{2}}}} \right) \\
\therefore F= Mg\tan \dfrac{\theta }{2}$

So, the minimum value of force $F$ must be $Mg\tan \dfrac{\theta }{2}$ in order to move the block upward.

Note: It must be noted that the given question stated that the plane is frictionless. If there is friction on the surface, it will oppose the motion of the body. Thus, we have calculated a force in opposite direction to the force required to move the body upwards to find the equation of the forces that balances each other.