Question

Milk world Ltd. Is a government-owned milk distribution centre. Earlier they used to distribute milk in bottles as shown in the figure for rupees 8 per bottle. Now they have decided to reduce the price per bottle by 50 paise by reducing the size of the bottle. However, they do not want their old customers to notice this change in size of the bottle so they plan to reduce the circumference of the opening of the bottle without changing the height of the bottle. What is the new circumference of the opening?
 $
  \left( {\text{A}} \right)6\pi {\text{cm}} \\
  \left( {\text{B}} \right)8\pi {\text{cm}} \\
  \left( {\text{C}} \right)3.5\pi {\text{cm}} \\
  $
 $ \left( {\text{D}} \right) $ None of these

Answer 1

Hint: Start the solution by listing the information given in the diagram. Try to find out the volume of the bottle by finding volumes of different part separately and then adding them. Find the %reduction and hence find the %reduction of the entire bottle. And hence find the circumference.

Complete step-by-step answer:
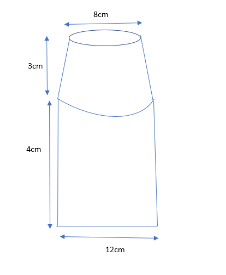
First we will try to note down all the information about the original bottle from the given figure.
The diameter of cylinder = 12cm $ \Rightarrow $ radius of cylinder=r = 6cm
Height of the cylinder = h1=4cm
The diameter of the top of the frustum = 8cm $ \Rightarrow $ radius of top frustum=R = 4cm
Height of the frustum = h2 = 3cm
Volume of the cylinder = $ \pi {r^2}{h_1} $
 $
   = \pi \times 6 \times 6 \times 4 \\
   = 144\pi \;
  $
Volume of the frustum = $ \dfrac{1}{3}\pi {h_2}({r^2} + {R^2} + \left( {r.R} \right) $
 $
   = \dfrac{1}{3}\pi \times 3 \times ({6^2} + {4^2} + \left( {6 \times 4} \right) \\
   = 76\pi \;
  $
volume of the bottle = Volume of the cylinder + Volume of the frustum
 $
   = 144\pi + 76\pi \\
   = 220\pi \;
  $
% reduction in price will be $ \dfrac{{0.50}}{8} \times 100 = \dfrac{{25}}{4}\% $
Hence the reduction in frustum volume will be $ 76\pi - \dfrac{{25}}{4}\% $ of $ 220\pi $
 $
   = 76\pi - \dfrac{{25}}{4}\% \times 220\pi \\
   = 76\pi - \dfrac{{25}}{{400}} \times 220\pi \\
   = 76\pi - \dfrac{{55\pi }}{4} \\
   = \dfrac{{249\pi }}{4} \;
  $
Hence the volume of the reduced conical frustum = $ \dfrac{{249\pi }}{4} $
 $
   \Rightarrow \dfrac{1}{3}\pi \times 3 \times \left( {{6^2} + {r^2} + 6r} \right) = \dfrac{{249\pi }}{4} \\
   \Rightarrow 144 + 4{r^2} + 24r = 249 \\
   \Rightarrow 4{r^2} + 24r - 105 = 0 \;
  $
Hence by factoring the above equation we get the value of r as 2.94cm
Hence the circumference = $ 2\pi r = 2\pi \times 2.94 = 5.88\pi \approx 6\pi $
Hence the correct option to the above question will be option A
So, the correct answer is “Option A”.

Note: This kind of problems have to be dealt with by first obtaining the value from the entire information given and later trying to find out what is to be obtained. Solving the sum by separating the diagram also helps a lot as in the above problem. To avoid confusion one has to list the formulas of each shape differently.