Question

Match the items in the left column with the items in the right column

$\begin{align}
  & [a]\left( i \right)\to \left( b \right),\left( ii \right)\to \left( d \right),\left( iii \right)\to \left( a \right),\left( iv \right)\to \left( c \right) \\
 & [b]\left( i \right)\to \left( c \right),\left( ii \right)\to \left( a \right),\left( iii \right)\to \left( b \right),\left( iv \right)\to \left( d \right) \\
 & [c]\left( i \right)\to \left( b \right),\left( ii \right)\to \left( c \right),\left( iii \right)\to \left( a \right),\left( iv \right)\to \left( d \right) \\
 & [d]\left( i \right)\to \left( a \right),\left( ii \right)\to \left( c \right),\left( iii \right)\to \left( b \right),\left( iv \right)\to \left( d \right) \\
\end{align}$

Answer 1

Hint: Recall the various criteria for congruence and identify which rule should be applied to which example. Hence determine which example matches to which rule.

Complete step-by-step answer:

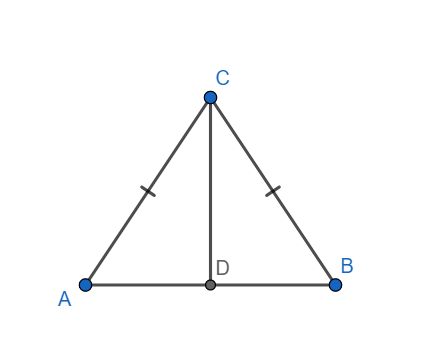
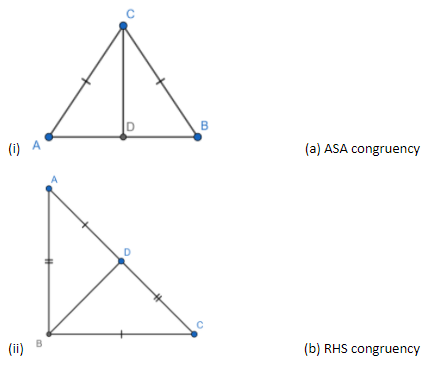
In triangles ACD and BCD, we have
AC = BC (Given)
$\angle CDA=\angle CDB$ (each 90)
CD = CD.
Hence we have $\Delta ADC\cong \Delta BDC$ by RHS congruence criterion.
Hence $\left( i \right)\to \left( b \right)$

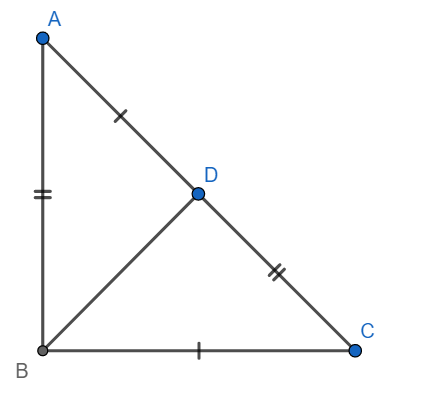
In triangles ABD and CDB, we have
AB = CD (Given)
AD = BC (Give)
BD = BD (Common side)
Hence $\Delta ABD\cong \Delta CDB$ by SSS congruence criterion.
Hence $\left( ii \right)\to \left( c \right)$

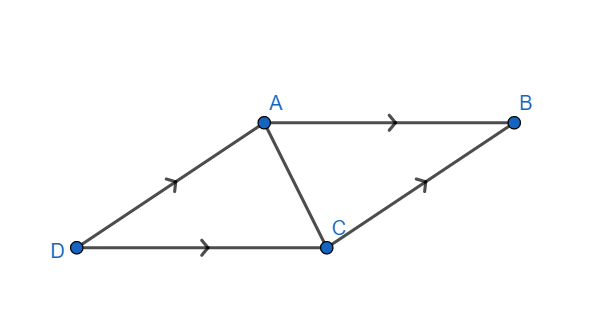
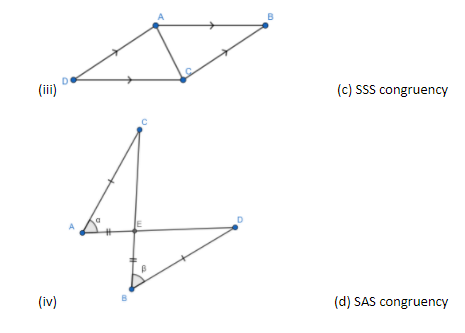
Since $AB\parallel DC,$ we have $\angle ACD=\angle CAB$ (alternate interior angles)
Similarly, since $AD\parallel CB,$ we have $\angle DAC=\angle ACB$
In triangles ADC and CBA, we have
$\angle ACD=\angle CAB$ (proved above)
AC = AC (common side)
$\angle DAC=\angle ACB$ (proved above)
Hence $\Delta ACD\cong \Delta CAB$ by ASA congruence criterion.
Hence $\left( iii \right)\to \left( a \right)$

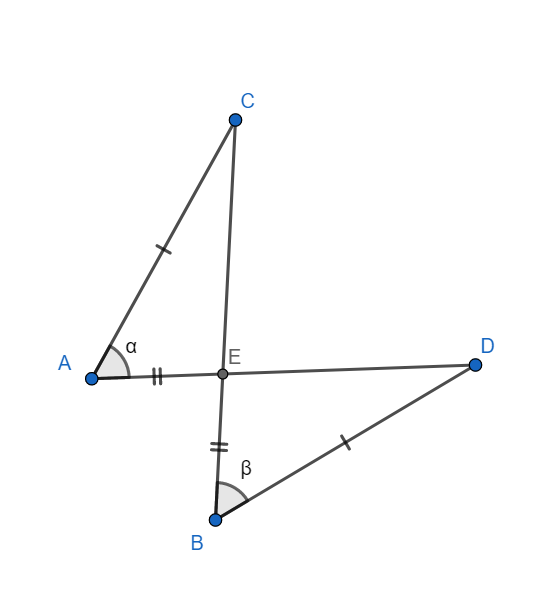
In triangles AEC and BED, we have
AC = BD (Given)
$\angle CAE=\angle EBD$ (Given)
AE = BE (Given)
Hence $\Delta AEC\cong \Delta BED$ by SAS congruence criterion
Hence $\left( iv \right)\to \left( d \right)$

So, the correct answer is “Option (c)”.

Note: In these types of questions, we need to think that what is given in the diagram and what can be derived. Hence we must understand which congruence rule should we apply to prove the triangles congruent. Also, we need to understand what various congruence criteria mean. Like SAS congruence condition is valid when the angle is the angle included between the two sides. Many students fail to realise that and hence prove triangles are congruent in an incorrect way.