
Match the following lists:
1) $f:R\to R$ defined by $f\left( x \right)=ax+b$ is $a\ne 0$ a) injection but not surjection 2) $f:R\to R$ defined by $f\left( x \right)=\left[ x \right]$ is b) surjection but not injection 3) $f:R\to \left[ 0,\infty \right)$ defined by $f\left( x \right)=\left| x \right|$ is c) bijection 4) $f:N\to N$ defined $f\left( x \right)={{x}^{3}}$ is d) neither injection nor bijection
(A) $1\to c$, $2\to d$, $3\to a$, $4\to b$
(B) $1\to c$, $2\to d$, $3\to b$, $4\to a$
(C) $1\to d$, $2\to c$, $3\to b$, $4\to a$
(D) $1\to d$, $2\to c$, $3\to a$, $4\to b$
| 1) $f:R\to R$ defined by $f\left( x \right)=ax+b$ is $a\ne 0$ | a) injection but not surjection |
| 2) $f:R\to R$ defined by $f\left( x \right)=\left[ x \right]$ is | b) surjection but not injection |
| 3) $f:R\to \left[ 0,\infty \right)$ defined by $f\left( x \right)=\left| x \right|$ is | c) bijection |
| 4) $f:N\to N$ defined $f\left( x \right)={{x}^{3}}$ is | d) neither injection nor bijection |
Answer
557.4k+ views
Hint: We start solving the problem by recalling the definitions of injection, surjection and bijection functions. We then take each function and check they were satisfying the conditions of one-one function first and then check whether the range of the function is equal to its co-domain to check whether the given function is surjection. We then match them with the correct option of the other column to get the required answer.
Complete step-by-step answer:
According to the problem, we are asked to match the two given columns.
Let us first recall the definitions of injection and surjection.
We know that if a function ‘f’ is defined as injection, then every element in the domain has a different image of the co-domain.
We know that if a function ‘f’ is defined as surjection, then the range of the function is equal to the co-domain.
We know that if a function ‘f’ is defined as bijection if it is both injection and bijection.
Let us now check 1).
We have given the function $f:R\to R$ defined by $f\left( x \right)=ax+b$$\left( a\ne 0 \right)$.
Let us assume $f\left( {{x}_{1}} \right)=f\left( {{x}_{2}} \right)$, where ${{x}_{1}}$, ${{x}_{2}}$ be any two elements in the domain of ‘f’.
So, we have $a{{x}_{1}}+b=a{{x}_{2}}+b$.
$\Rightarrow a{{x}_{1}}=a{{x}_{2}}$.
$\Rightarrow {{x}_{1}}={{x}_{2}}$. So, the values of ${{x}_{1}}$ and ${{x}_{2}}$ should be same in order to have same images.
So, $f\left( x \right)=ax+b$$\left( a\ne 0 \right)$ is an injection.
Now, let us assume y be an element in the co-domain of the function which satisfies $y=ax+b$.
$\Rightarrow y-b=ax$.
$\Rightarrow x=\dfrac{y-b}{a}$.
Now, let us find $f\left( x \right)$.
$\Rightarrow f\left( x=\dfrac{y-b}{a} \right)=a\left( \dfrac{y-b}{a} \right)+b$.
$\Rightarrow f\left( x \right)=y-b+b$.
$\Rightarrow f\left( x \right)=y$ ---(i).
We know that $f\left( x \right)$ is the range of the function. From equation (i), we can see that the range of the function is equal to its co-domain. So, the given function is also surjective.
So, the given function is both injection and surjection which means that the given function is a bijection.
∴ $1\to c$.
Now, let us check 2)
We have given the function $f:R\to R$ defined by $f\left( x \right)=\left[ x \right]$.
We know that the greatest integer function $\left[ x \right]$ gives the greatest integer that is just less than or equal to the number x. So, it neglects all real numbers except integers which tells us that the range is not equal to co-domain.
So, the function $f\left( x \right)=\left[ x \right]$ is not a surjection.
We can see that $f\left( 0.1 \right)=\left[ 0.1 \right]=0$ and $f\left( 0.01 \right)=\left[ 0.01 \right]=0$, which tells that different elements of domain have same images which contradicts the property of injection.
So, the function $f\left( x \right)=\left[ x \right]$ is not an injection.
We have found that the function $f\left( x \right)=\left[ x \right]$ is neither an injection nor a surjection.
∴ $2\to d$.
Now, let us check 3)
We have given function $f:R\to \left[ 0,\infty \right)$ defined by $f\left( x \right)=\left| x \right|$.
We know that the range of the $\left| x \right|$ is greater than or equal to 0 i.e., $\left[ 0,\infty \right)$ for any value of $x\in R$. We can see that this range is equal to the given co-domain, which makes the given function $f\left( x \right)=\left| x \right|$ a surjection.
We know that the modulus function of x is defined as $\left| x \right|=\left\{ \begin{matrix}
x,\text{ }if\text{ }x>0 \\
-x,\text{ }if\text{ }x<0 \\
0,\text{ }if\text{ }x=0 \\
\end{matrix} \right.$.
Now, we have $f\left( 1 \right)=\left| 1 \right|=1$ and $f\left( -1 \right)=\left| -1 \right|=-\left( -1 \right)=1$, which tells that different elements of domain have the same images which contradicts the property of injection.
So, we have found that the function $f\left( x \right)=\left| x \right|$ is not an injection.
We have found that the function $f\left( x \right)=\left| x \right|$ is a surjection not an injection.
∴ $3\to b$.
Now, let us check 4)
We have given the function $f:N\to N$ defined $f\left( x \right)={{x}^{3}}$.
Let us differentiate the function $f\left( x \right)={{x}^{3}}$.
We have ${{f}^{'}}\left( x \right)=\dfrac{d}{dx}\left( {{x}^{3}} \right)=3{{x}^{2}}$. We know that ${{x}^{2}}$ is strictly greater than 0 over N. This makes the given function $f\left( x \right)={{x}^{3}}$ in N. We know that strictly increasing functions over a given domain injections.
So, the given function $f\left( x \right)={{x}^{3}}$ is an injection.
Now, let us assume $f\left( x \right)=3$.
$\Rightarrow {{x}^{3}}=3$.
$\Rightarrow x=\sqrt[3]{3}$, which is an irrational number not a natural number. We can see that every natural number is not in the range of the function $f\left( x \right)={{x}^{3}}$, which makes range not equal to given co-domain.
So, the given function $f\left( x \right)={{x}^{3}}$ is not a surjection.
We have found that the given function $f\left( x \right)={{x}^{3}}$ is an injection not a surjection.
∴ $4\to a$.
So, the correct answer is “Option B”.
Note: We can also solve the problem by drawing the plot of the given function and checking the domain of the range of the given function from the plot itself. We can see one of such solving process as shown below:
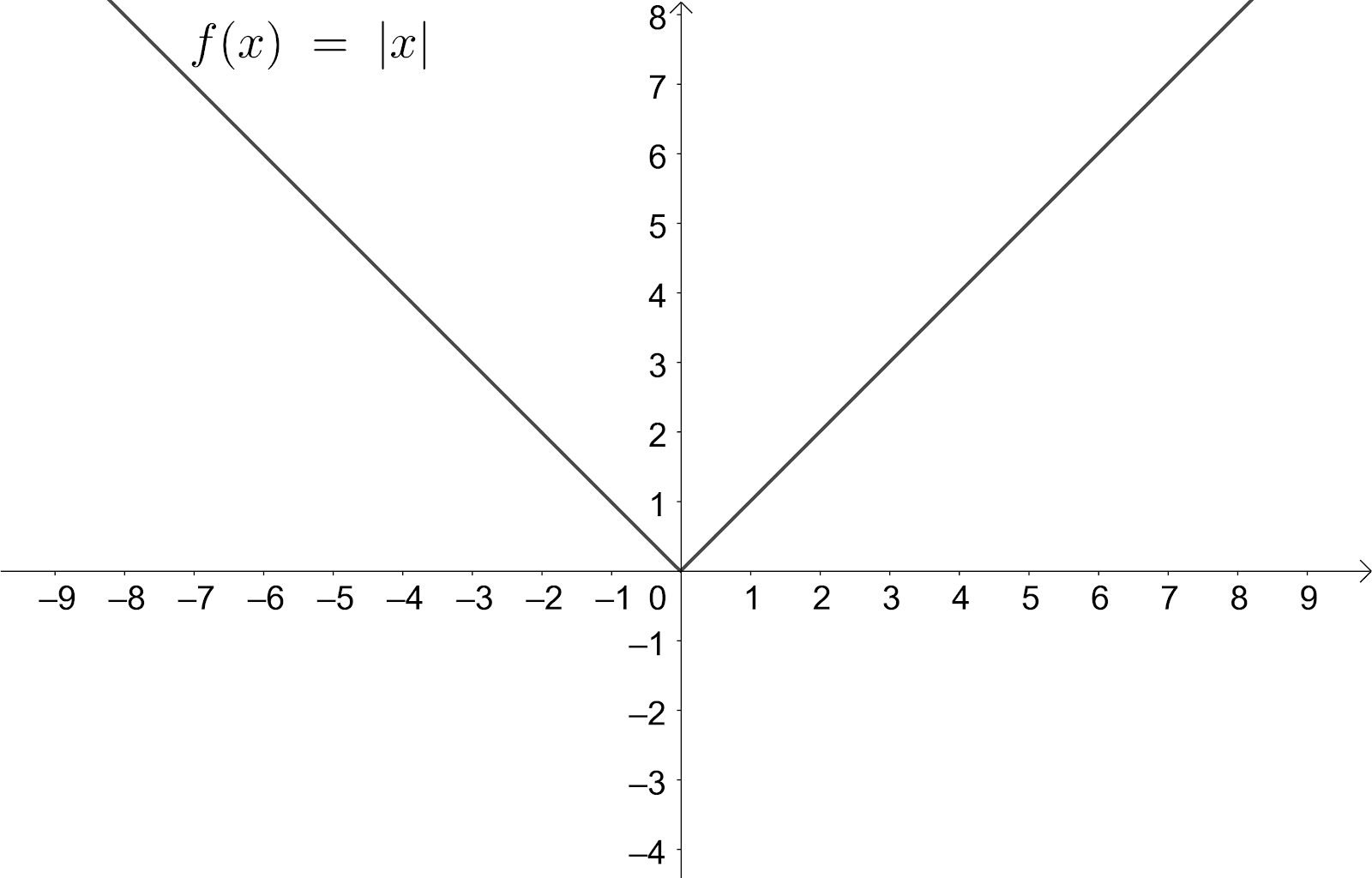
We can see that the function is having different images for different values of x, but the images are only positive real values which are not equal to the given co-domain. Similarly, we can expect problems to check whether the given functions $f\left( x \right)=\left\{ x \right\}$ where $\left\{ . \right\}$ is fractional part function and $g\left( x \right)=\left( x \right)$ where $\left( . \right)$ is L.I.F (Least Integer Function).
Complete step-by-step answer:
According to the problem, we are asked to match the two given columns.
Let us first recall the definitions of injection and surjection.
We know that if a function ‘f’ is defined as injection, then every element in the domain has a different image of the co-domain.
We know that if a function ‘f’ is defined as surjection, then the range of the function is equal to the co-domain.
We know that if a function ‘f’ is defined as bijection if it is both injection and bijection.
Let us now check 1).
We have given the function $f:R\to R$ defined by $f\left( x \right)=ax+b$$\left( a\ne 0 \right)$.
Let us assume $f\left( {{x}_{1}} \right)=f\left( {{x}_{2}} \right)$, where ${{x}_{1}}$, ${{x}_{2}}$ be any two elements in the domain of ‘f’.
So, we have $a{{x}_{1}}+b=a{{x}_{2}}+b$.
$\Rightarrow a{{x}_{1}}=a{{x}_{2}}$.
$\Rightarrow {{x}_{1}}={{x}_{2}}$. So, the values of ${{x}_{1}}$ and ${{x}_{2}}$ should be same in order to have same images.
So, $f\left( x \right)=ax+b$$\left( a\ne 0 \right)$ is an injection.
Now, let us assume y be an element in the co-domain of the function which satisfies $y=ax+b$.
$\Rightarrow y-b=ax$.
$\Rightarrow x=\dfrac{y-b}{a}$.
Now, let us find $f\left( x \right)$.
$\Rightarrow f\left( x=\dfrac{y-b}{a} \right)=a\left( \dfrac{y-b}{a} \right)+b$.
$\Rightarrow f\left( x \right)=y-b+b$.
$\Rightarrow f\left( x \right)=y$ ---(i).
We know that $f\left( x \right)$ is the range of the function. From equation (i), we can see that the range of the function is equal to its co-domain. So, the given function is also surjective.
So, the given function is both injection and surjection which means that the given function is a bijection.
∴ $1\to c$.
Now, let us check 2)
We have given the function $f:R\to R$ defined by $f\left( x \right)=\left[ x \right]$.
We know that the greatest integer function $\left[ x \right]$ gives the greatest integer that is just less than or equal to the number x. So, it neglects all real numbers except integers which tells us that the range is not equal to co-domain.
So, the function $f\left( x \right)=\left[ x \right]$ is not a surjection.
We can see that $f\left( 0.1 \right)=\left[ 0.1 \right]=0$ and $f\left( 0.01 \right)=\left[ 0.01 \right]=0$, which tells that different elements of domain have same images which contradicts the property of injection.
So, the function $f\left( x \right)=\left[ x \right]$ is not an injection.
We have found that the function $f\left( x \right)=\left[ x \right]$ is neither an injection nor a surjection.
∴ $2\to d$.
Now, let us check 3)
We have given function $f:R\to \left[ 0,\infty \right)$ defined by $f\left( x \right)=\left| x \right|$.
We know that the range of the $\left| x \right|$ is greater than or equal to 0 i.e., $\left[ 0,\infty \right)$ for any value of $x\in R$. We can see that this range is equal to the given co-domain, which makes the given function $f\left( x \right)=\left| x \right|$ a surjection.
We know that the modulus function of x is defined as $\left| x \right|=\left\{ \begin{matrix}
x,\text{ }if\text{ }x>0 \\
-x,\text{ }if\text{ }x<0 \\
0,\text{ }if\text{ }x=0 \\
\end{matrix} \right.$.
Now, we have $f\left( 1 \right)=\left| 1 \right|=1$ and $f\left( -1 \right)=\left| -1 \right|=-\left( -1 \right)=1$, which tells that different elements of domain have the same images which contradicts the property of injection.
So, we have found that the function $f\left( x \right)=\left| x \right|$ is not an injection.
We have found that the function $f\left( x \right)=\left| x \right|$ is a surjection not an injection.
∴ $3\to b$.
Now, let us check 4)
We have given the function $f:N\to N$ defined $f\left( x \right)={{x}^{3}}$.
Let us differentiate the function $f\left( x \right)={{x}^{3}}$.
We have ${{f}^{'}}\left( x \right)=\dfrac{d}{dx}\left( {{x}^{3}} \right)=3{{x}^{2}}$. We know that ${{x}^{2}}$ is strictly greater than 0 over N. This makes the given function $f\left( x \right)={{x}^{3}}$ in N. We know that strictly increasing functions over a given domain injections.
So, the given function $f\left( x \right)={{x}^{3}}$ is an injection.
Now, let us assume $f\left( x \right)=3$.
$\Rightarrow {{x}^{3}}=3$.
$\Rightarrow x=\sqrt[3]{3}$, which is an irrational number not a natural number. We can see that every natural number is not in the range of the function $f\left( x \right)={{x}^{3}}$, which makes range not equal to given co-domain.
So, the given function $f\left( x \right)={{x}^{3}}$ is not a surjection.
We have found that the given function $f\left( x \right)={{x}^{3}}$ is an injection not a surjection.
∴ $4\to a$.
So, the correct answer is “Option B”.
Note: We can also solve the problem by drawing the plot of the given function and checking the domain of the range of the given function from the plot itself. We can see one of such solving process as shown below:

We can see that the function is having different images for different values of x, but the images are only positive real values which are not equal to the given co-domain. Similarly, we can expect problems to check whether the given functions $f\left( x \right)=\left\{ x \right\}$ where $\left\{ . \right\}$ is fractional part function and $g\left( x \right)=\left( x \right)$ where $\left( . \right)$ is L.I.F (Least Integer Function).
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 8 Maths: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

Which animal has three hearts class 11 biology CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




