Question

Mary says, “the number I am thinking is divisible by 2 or it is divisible by 3”. This statement is false if the number Mary is thinking of is:
a. 6
b. 8
c. 11
d. 15

Answer 1

Hint: This question involves the concept of mathematical reasoning. Given statement in the question is an added statement of two different statements with disjunction (or). We will check both the statements separately for each option whether they are true or false and then accordingly, we will be able to say whether the given statement is true or false and we will refer to the truth table for disjunction (or) to do so. We will check all the options one by one for the answer.

Complete step-by-step answer:
This question is related to mathematical reasoning. And, here we have the disjunction as (or). So, we have the truth table for (or) as follows.

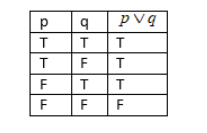
Now, let us consider the statement 1, which is, “the number is divisible by 2” as p and the statement 2, which is, “the number is divisible by 3” as q.
Now, the given equation added by disjunction (or), “the number is divisible by 2 or it is divisible by 3” is $p\vee q$.
According to the question, we have to check when the given statement is false. So, we will check all the options one by one.
First we will check option (a), that is, 6.
The number is 6.
Statement 1: “The number is divisible by 2”. That is,
6 is divisible by 2. And this is true, so p is true.
Statement 2: “The number is divisible by 3”. That is,
6 is divisible by 3. And this is true, so q is true.
So, we get p and q are true. So, according to the truth table, we get that $p\vee q$ is also true. So, this option is not correct.
Now let us see option (b).
The number is 8.
Statement 1: “The number is divisible by 2”. That is,
8 is divisible by 2. And this is true, so p is true.
Statement 2: “The number is divisible by 3”. That is,
8 is divisible by 3. And this is false, so q is false.
As p is true and q is false, according to the truth table, we get that $p\vee q$ is true. So, this option is also not correct.
Now, let us see option (c).
The number is 11.
Statement 1: “The number is divisible by 2”. That is,
11 is divisible by 2. And this is false, so p is false.
Statement 2: “The number is divisible by 3”. That is,
11 is divisible by 3. And this is false, so q is false.
As p and q are false, according to the truth table, $p\vee q$ is also false. So, this is the correct answer.
Now, let us see option (d).
The number is 15.
Statement 1: “The number is divisible by 2”. That is,
15 is divisible by 2. And this is false, so p is false.
Statement 2: “The number is divisible by 3”. That is,
15 is divisible by 3. And this is true, so q is true.
As p is false and q is true, according to the truth table, $p\vee q$ is true. So, this option is wrong.
Therefore, we get that the statement $p\vee q$ will be false when Mary is thinking of the number 11.
Hence, option (c) is the correct answer.

Note: In this type of questions, the students may make mistakes as they get confused between (and) and (or). So, it is to be noted that, (or) will be false only when both the statements are false and (and) will be only true when both the statements are true.