Question

Man is eating a pizza. During the first day he eats half of the pizza. On the second day, he eats \[{{\dfrac{1}{3}}^{rd}}\] of the remaining part of the pizza. The third day he eats \[{{\dfrac{1}{4}}^{th}}\] of what is left and 4th day he eats \[{{\dfrac{1}{5}}^{th}}\] of what still remains. He then stops because the last piece was not fresh. What fraction of the original pizza is still available?
A. 0.25
B. \[\dfrac{1234}{2345}\]
C. 0.12345
D. \[\dfrac{1}{5}\]

Answer 1

Hint: First of all we have to assume the total amount of pizza. After that we can find the portion he eats on the first day. Then by removing it from the total amount of pizza we can get the remaining part. Similarly we have to find the amount of day 2 day 3 and day 4 by calculating the portion and removing it from the rest of the pizza. If we do this till day 4 we can find the remaining part of the pizza.

Complete step-by-step answer:
Let us assume that the total pizza is 1.
During the first day the man eats the half of the pizza, meaning,
\[1\times \dfrac{1}{2}\].
So the remaining pizza after first day is
\[\begin{align}
  & \left( 1-\dfrac{1}{2} \right) \\
 & \Rightarrow \dfrac{1}{2} \\
\end{align}\]

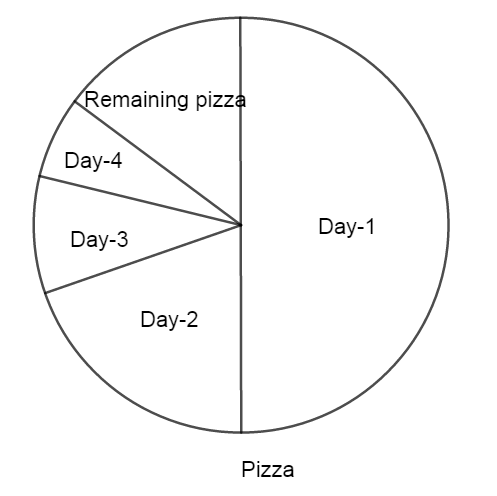
We can represent the pizza eaten by this diagram.
On the second day, the man eats \[{{\dfrac{1}{3}}^{rd}}\] of the remaining part of the pizza, meaning,
\[\begin{align}
  & \dfrac{1}{2}\times \dfrac{1}{3} \\
 & \Rightarrow \dfrac{1}{6} \\
\end{align}\]
We will get the remaining pizza after second day as,
\[\left( \dfrac{1}{2}-\dfrac{1}{6} \right)\]
We know the LCM of 2 and 3 is 6. Now,
\[\begin{align}
  & \Rightarrow \dfrac{3-2}{6} \\
 & \Rightarrow \dfrac{2}{6} \\
 & \Rightarrow \dfrac{1}{3} \\
\end{align}\]
The third day the man eats \[{{\dfrac{1}{4}}^{th}}\] of what is left, meaning,
\[\begin{align}
  & \dfrac{1}{3}\times \dfrac{1}{4} \\
 & \Rightarrow \dfrac{1}{12} \\
\end{align}\]
After subtracting \[\dfrac{1}{12}\] from \[\dfrac{1}{3}\] we will get the remaining pizza after second day as,
\[\left( \dfrac{1}{3}-\dfrac{1}{12} \right)\]
We know the LCM of 3 and 12 is 12. Now,
\[\begin{align}
  & \Rightarrow \dfrac{4-1}{12} \\
 & \Rightarrow \dfrac{3}{12} \\
 & \Rightarrow \dfrac{1}{4} \\
\end{align}\]
Similarly on the fourth day the man eats \[{{\dfrac{1}{5}}^{th}}\] of what still remains.
\[\begin{align}
  & \dfrac{1}{4}\times \dfrac{1}{5} \\
 & \Rightarrow \dfrac{1}{20} \\
\end{align}\]

After eating \[{{\dfrac{1}{5}}^{th}}\] Part of pizza remaining pizza after fourth day will be,
\[\left( \dfrac{1}{4}-\dfrac{1}{20} \right)\]
We know the LCM of 4 and 20 is 20. Now,
\[\begin{align}
  & \Rightarrow \dfrac{5-1}{20} \\
 & \Rightarrow \dfrac{4}{20} \\
 & \Rightarrow \dfrac{1}{5} \\
\end{align}\]
He stopped eating after that because the last piece was not fresh.
\[{{\dfrac{1}{5}}^{th}}\] fraction (Option D) of the original pizza is still available.

Note: Students get confused by the question so try to visualize the problem as shown in the diagram shown. They may forget to subtract the eating portion value from the remaining total amount of pizza.
If they forget to do that then the math will be wrong. Try to use brackets when subtracting.