Question

How many lines of symmetry does the following given figure (Scalene triangle) have ?

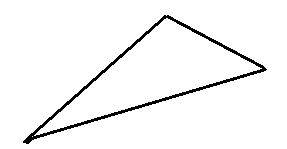
A. 3
B. 2
C. 1
D. 0

Answer 1

Hint: We had to only use the definition of line of symmetry for any shape which says that if any figure has x number of lines of symmetry then there will be x possible lines which divide that figure into two equal parts (i.e. mirror images). And then check the number of lines in the scalene triangle which divide it into two mirror images.

Complete step-by-step answer:
Now as we know that there are three main types of triangle and that were,
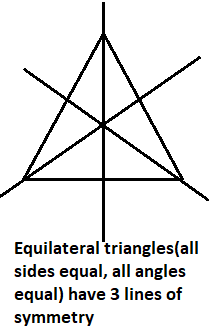
Equilateral triangle is the triangle whose all three sides are equal.
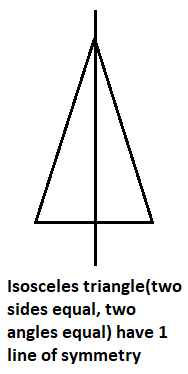
Isosceles triangle is the triangle whose length of two sides are the same and the third side has a different length.
And, scalene triangle is the triangle whose length of all the sides are different.
So, now we are given a scalene triangle and asked to find the number of lines of symmetry in that triangle.
As we know that line of symmetry for a triangle is a line which divides the triangle into two mirror images.
Or we can say if we fold the image from the line then two parts on the opposite side of the lines coincide with each other.
So, let us plot and find lines of symmetry for all types of triangles.

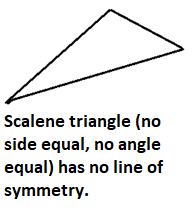
As we know that scalene triangles have all different sides and angles. So, there is no such line possible in the scalene triangle which divides it into two mirror images.
Hence, the correct option will be D.

Note:- Whenever we come up with this type of problem then we first write the definition of all types of triangles and line of symmetry and then plot figures for all types of triangles and check how many numbers of such lines can be drawn on the triangle which divide it into two mirror images. This will be the easiest and most efficient way to find the solution to the problem.