Question

How many lines of symmetry does a circle have?
(a) 1
(b) 2
(c) 3
(d) infinite

Answer 1

Hint: The definition of the lines of symmetry would be the hint here. The lines of symmetry are the lines which divide the shape they pass through into two equal parts.

Complete step-by-step answer:
So a regular polygon of n sides will have 2n lines of symmetry since the line through every vertex can divide it into two equal parts. So a regular hexagon will have 12 lines of symmetry, a regular heptagon will have 14 lines of symmetry, a regular octagon will have 16 lines of symmetry, a regular icosagon will have 40 lines of symmetry and so on.

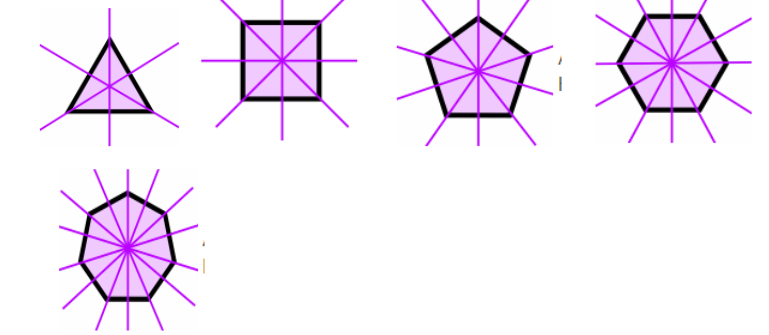
As we can see from the above figures, the number of the lines of symmetry vary with the number of sides the polygon has.
Now let us come to the case of the circle. It does not have any sides which cannot be distinctly shown.
Actually it has an infinite number of sides. That is the reason the surface line of the circle, more accurately the circumference or the perimeter of the circle looks smooth and without any corner points.
So as we learnt earlier the number of lines of symmetry vary as 2n if the number of sides of the polygon are n.
But the circle has an infinite number of sides. So it should have infinitely many lines of symmetry.
So the option(d) is the correct one.
Note: Alternatively, the lines of symmetry can be defined as the lines which when drawn perpendicular to any side of the polygon will pass through the centre of the polygon. But in a circle a line drawn at any angle will always pass through the centre. Thus for a circle an infinite number of lines will satisfy the equation. Thus the lines of symmetry for a circle are infinite.