Question

Let ${x^2} + {y^2} - 4x - 2y - 11 = 0$ be a circle, A pair of tangents from point (4,5) with a pair of radii form a quadrilateral of area?

Answer 1

Hint: Start by drawing the diagram , rearrange the given equation of circle and find out the centre and radius , calculate area of quadrilateral using the formula Area = radius x length of the tangent. Find out the length of the tangent and substitute the values to get the desired area.

Complete step-by-step answer:

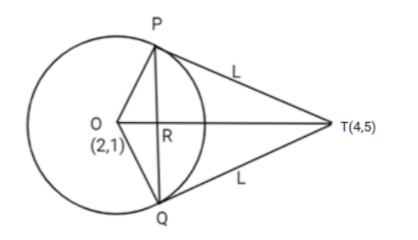
Given,
${x^2} + {y^2} - 4x - 2y - 11 = 0$
On re-arranging the terms, we get
${(x - 2)^2} + {(y - 1)^2} = {4^2}$
On comparing with ${{\text{(}}x - h)^2} + {(y - k)^2} = {r^2}$, we get
$h = 2,k = 1,r = 4$
Centre (2,1) and radius = r = 4
Now, Area of quadrilateral TPOQ will be
${\text{Area = Length of the tangent }} \times {\text{ Radius}} \to {\text{eqn(1)}}$
Now , let us find out the length of tangent from an external point (a,b) , found by
$\sqrt {{S_1}} = \sqrt {{a^2} + {b^2} - 2ha - 2kb + c} $
Length of tangent ${\text{ = }}\sqrt {{4^2} + {5^2} - 4 \cdot 4 - 2 \cdot 5 - 11} $
$
   = \sqrt {16 + 25 - 16 - 10 - 11} \\
   = \sqrt {25 - 21} \\
   = \sqrt 4 \\
   = 2 \\
$
Now, From eqn. (1)
$
  {\text{Area = 4}} \times {\text{2}} \\
  {\text{Area = 8 sq unit}}{\text{.}} \\
$

Note: All the formulas related to circles in general and parametric form must be well known in order to solve such similar questions. Attention is to be given while substituting values or comparing the values.
Alternative :
\[{\text{Area of quadrilateral = 2}} \times {\text{Area of }}\Delta {\text{TOQ}}\]
Area of \[\Delta {\text{TOQ}} = \dfrac{1}{2} \times {\text{OQ}} \times {\text{QT}}\]
Area of \[\Delta {\text{TOQ}} = \dfrac{1}{2} \times 4 \times 2 = 4\]sq. units
Area of quadrilateral = \[{\text{2}} \times 4 = 8\]sq. units