Question

Let X, Y, Z be respectively the areas of a regular pentagon, regular hexagon and regular heptagon which are inscribed in a circle of radius 1. Then,
A. \[\dfrac{X}{5} < \dfrac{Y}{6} < \dfrac{Z}{7}\ and\ X < Y < Z\]
B. \[\dfrac{X}{5} < \dfrac{Y}{6} < \dfrac{Z}{7}\ and\ X > Y > Z\]
C. \[\dfrac{X}{5} > \dfrac{Y}{6} > \dfrac{Z}{7}\ and\ X > Y > Z\]
D. \[\dfrac{X}{5} > \dfrac{Y}{6} > \dfrac{Z}{7}\ and\ X < Y < Z\]

Answer 1

Hint: We will find the area of regular pentagon, regular hexagon and regular heptagon individually and then compare the obtained result to the given relations in options. The regular polygons can be divided into triangles. The area of regular polygons can be found by multiplying the number of sides and area of one triangle contained in it.

Complete step by step solution:
Given that,
X, Y, Z are the areas of a regular pentagon, regular hexagon and regular heptagon and we have to find the correct relation between these three regular polygons respectively.
The regular polygons can be divided into triangles. The area of regular polygons can be found by multiplying the number of sides and area of one triangle contained in it.
Let us consider the case of regular pentagon first. It is said in the question that a regular pentagon is inscribed in a circle of radius 1. So, we can draw a figure with all the details as shown below;

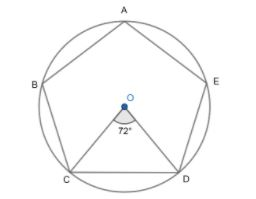
We know that an area of a regular pentagon can be divided into 5 equal triangles of the same area.
So, Pentagon (ABCD) area \[=\text{ }5\times \left( area\text{ }of\Delta OCD \right)\].
\[Area\text{ }of\Delta OCD\left( base=\sin 72{}^\circ \ \And \ apothem=1 \right)=\dfrac{1}{2}\times base\times height=\dfrac{base\times apothem}{2}\]
The radius of the incircle is the apothem of the regular polygon and here the height of the triangle is apothem of the regular polygon.
So, on putting the values of base and apothem, we get,
$Area\ of\ \Delta OCD=\dfrac{1}{2}\times 1\times \sin 72{}^\circ $
$\begin{align}
  & =\dfrac{1}{2}\times 0.951 \\
 & =0.951 \\
\end{align}$
So, the area of regular pentagon (ABCDE) \[=\text{ }5\times \left( area\text{ }of\Delta OCD \right)\]
$\begin{align}
  & =\dfrac{5\times 0.951}{2} \\
 & =2.377 \\
\end{align}$
Similarly, we will find the area of a regular hexagon (ABCDEF). It is said in the question that a regular hexagon is inscribed in a circle of radius 1. So, we can draw a figure with all the details as shown below;

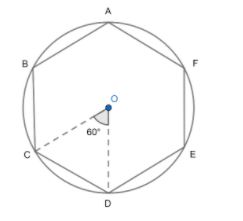
Area of regular hexagon (ABCDEF) \[=\text{ 6}\times \left( area\text{ }of\Delta OCD \right)\]
\[Area\text{ }of\Delta OCD\left( base=\sin 60{}^\circ \ \And \ apothem=1 \right)=\dfrac{1}{2}\times base\times height=\dfrac{base\times apothem}{2}\]
So, on putting the values of base and apothem, we get,
$Area\ of\ \Delta OCD=\dfrac{1}{2}\times \sin 60{}^\circ \times 1$
$\begin{align}
  & =\dfrac{1}{2}\times \dfrac{\sqrt{3}}{2} \\
 & =\dfrac{\sqrt{3}}{4} \\
\end{align}$
So, the area of regular hexagon (ABCDEF) \[=\text{ 6}\times \left( area\text{ }of\Delta OCD \right)\]
$\begin{align}
  & =6\times \dfrac{\sqrt{3}}{4} \\
 & =\dfrac{10.26}{4} \\
 & =2.565 \\
\end{align}$
Similarly, we will find the area of regular heptagon (ABCDEFG). It is said in the question that regular heptagon is inscribed in a circle of radius 1. So, we can draw a figure with all the details as shown below;

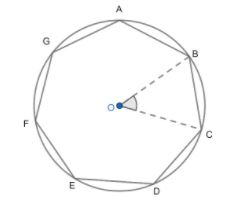
Area of regular heptagon (ABCDEFG) \[=\text{ 7}\times \left( area\text{ }of\Delta OCB \right)\]
\[Area\text{ }of\Delta OCB\left( base=\dfrac{\sin \left( 2\pi \right)}{7}\ \And \ apothem=1 \right)=\dfrac{1}{2}\times base\times height=\dfrac{1}{2}\times base\times apothem\]
So, on putting the values of base and apothem, we get,
$Area\ of\ \Delta OCB=\dfrac{1}{2}\times 1\times \sin \left( \dfrac{2\pi }{7} \right)$
$=\dfrac{1}{2}\times \sin \left( \dfrac{2\pi }{7} \right)$
We know that $\sin \left( \dfrac{2\pi }{7} \right)=0.78183$.
So, on putting $\sin \left( \dfrac{2\pi }{7} \right)$as 0.78183, we get,
$\begin{align}
  & =\dfrac{1}{2}\times 0.78183 \\
 & =0.390915 \\
\end{align}$
So, the area of regular heptagon (ABCDEFG) \[=7\times \left( 0.390915 \right)=2.736\]
So, the area of regular heptagon (ABCDEFG) will be 2.736.
So, we have X = 2.377, Y = 2.565 and Z = 2.736.
From this value we have,
2.377 < 2.565 < 2.736
X < Y < Z
Also,
$\begin{align}
  & \dfrac{2.377}{5}>\dfrac{2.565}{6}>\dfrac{2.736}{7} \\
 & Or,\ \dfrac{X}{5}>\dfrac{Y}{6}>\dfrac{Z}{7} \\
\end{align}$
So, we can clearly say that option (D) is the correct answer.

So, the correct answer is “Option (D)”.

Note: We can also solve this question using an alternate method. The steps for the alternate method are outlined below:
Step 1. Find the length of each side of every polygon individually by using geometry.
Step 2. Find the area of each polygon using their respective formula.
Step 3. Compare the results with the given options.