Question

Let us assume that a national roadway bridge over a canal will be in the form of an arc of a circle of radius $49m$. Without leaving the ground at the highest point, find out the maximum speed with which a vehicle can move? (Take,$g=9.8m{{s}^{-2}}$)
$\begin{align}
  & A.19.6m{{s}^{-1}} \\
 & B.40m{{s}^{-1}} \\
 & C.22m{{s}^{-1}} \\
 & D.\text{none of these} \\
\end{align}$

Answer 1

Hint: The maximum velocity with which a vehicle can move without leaving the ground at the highest point can be found by taking the square root of the product of the acceleration due to gravity and the radius of the circular path taken. Substitute the values in the equation. This will help you in answering this question.

Complete answer:

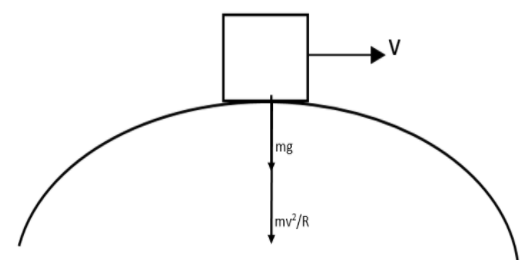
The centripetal force will be equivalent to the gravitational force on the body. That is,
$m\dfrac{{{v}^{2}}_{\max }}{R}=mg$
The maximum velocity with which a vehicle can move without leaving the ground at the highest point can be found by taking the square root of the product of the acceleration due to gravity and the radius of the circular path taken. This can be written as an equation given as,
${{v}_{\max }}=\sqrt{gR}$
It has been already mentioned in the question that the radius of the circular path taken by the vehicle be,
$R=49m$
The acceleration due to gravity has been mentioned as,
$g=9.8m{{s}^{-2}}$
Now let us substitute the values in the equation which can be shown as,
${{v}_{\max }}=\sqrt{9.8\times 49}=22m{{s}^{-1}}$
Therefore the maximum velocity with which a vehicle can move without leaving the ground at the highest point has been calculated.

The correct answer has been mentioned as option C.

Note:
The maximum safe speed is defined as the maximum possible speed a vehicle can move when they are traversing through a circular path. This speed is dependent upon the acceleration due to gravity, angle of inclination with the horizontal and radius of curvature. The maximum safe speed will not be dependent on the mass of the vehicle travelling.