Question

Let the function $ f\left( x \right)={{\left[ x \right]}^{2}}+\left[ x+1 \right]-3 $ where [.] denotes the greatest integer function. Then
A. $ f\left( x \right)\ne 0 $ for all real values of x.
B. $ f\left( x \right)=0 $ for only two real values of x.
C. $ f\left( x \right)=0 $ for infinite value of x.
D. $ f\left( x \right)=0 $ for no real value of x.

Answer 1

Hint: For this question, we will first use $ \left[ x+I \right]=\left[ x \right]+I $ to find quadratic function in the form of [x]. Then we will suppose [x] as y and solve the quadratic equation. Then we will use the value to find the value of [x]. After that, we will use the definition of the greatest integer function to find the range of x. Using that, we will find our answer.

Complete step by step answer:
Here we are given the function f(x) as $ f\left( x \right)={{\left[ x \right]}^{2}}+\left[ x+1 \right]-3 $ where [.] denotes the greatest integer function. We need to find the number of values of x when f(x) = 0.
Let us first simplify our given function.
 $ f\left( x \right)={{\left[ x \right]}^{2}}+\left[ x+1 \right]-3 $ .
We know that for a greatest integer function, $ \left[ x+I \right]=\left[ x \right]+I $ where I is any integer.
Therefore, let us change [x+1] into above form, we get $ f\left( x \right)={{\left[ x \right]}^{2}}+\left[ x \right]+1-3 $ .
Simplifying we get $ f\left( x \right)={{\left[ x \right]}^{2}}+\left[ x \right]-2 $ .
Now let us put f(x) = 0 to evaluate the value of x. We get, $ {{\left[ x \right]}^{2}}+\left[ x \right]-2=0 $ .
To avoid confusion let us suppose [x] as y, we get $ {{y}^{2}}+y-2=0 $ .
Using splitting the middle term method, we see that $ -2=\left( 2 \right)\left( -1 \right)\text{ and }1=2+\left( -1 \right) $ so we get,
\[\begin{align}
  & {{y}^{2}}+\left( 2-1 \right)y-2=0 \\
 & \Rightarrow {{y}^{2}}+2y-y-2=0 \\
 & \Rightarrow y\left( y+2 \right)-1\left( y+2 \right)=0 \\
 & \Rightarrow \left( y-1 \right)\left( y+2 \right)=0 \\
\end{align}\].
This implies that $ y-1=0\text{ and }y+2=0 $ or we can say y = 1, y = -2.
Putting values of y as [x], we get $ \left[ x \right]=1,\left[ x \right]=-2 $ .
Now according to the greatest integer function, [x] returns the largest integer less than or equal to x. So for [x] = 1, x should lie between 1 and 2 where it can be equal to 1 but not equal to 2. Therefore, for $ \left[ x \right]=1,1\le x\text{ }<\text{ }2\Rightarrow x\in \left[ 1,2 \right) $ .

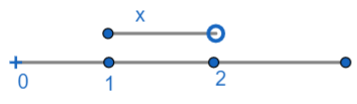
For $ \left[ x \right]=-2 $ .
x should lie between -1 and -2 where it can be equal to -2 but not equal to -1.
Therefore, for $ \left[ x \right]=-2,-2\le x\le -1\Rightarrow x\in \left[ -2,-1 \right) $ .

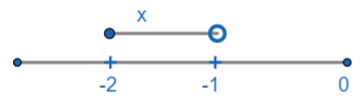
Combining both ranges of x, we get that $ x\in \left[ -2,-1 \right)\cup \left[ 1,2 \right) $ .
Now let us analyze our given options.
A. As we can see, there are real values for which $ f\left( x \right)=0 $ so option A is not correct.
B. In the interval [-2,-1) and [1,2) there exist infinite real numbers and not just two, so option B is not correct.
C. Option C is correct because there lies infinite values between found intervals for which $ f\left( x \right)=0 $ .
D. 1,2 are some examples of real values for which $ f\left( x \right)=0 $ so option D is not correct.
Hence option C is the correct answer.

Note:
Students should note that, while applying the definition of the greatest integer function on [x] = 1 make sure that 2 is not included and for [x] = -2, make sure that -1 is not included. Take care of signs while solving quadratic equations.