Question

Let $ S $ be the set of all functions $ f:[0,1] \to R $ , which are continuous on $ [0,1] $ and differentiable on $ (0,1). $ Then for every $ f $ in $ S $ , there exists a $ c \in (0,1) $ , depending on $ f $ , such that:
  $
  1.\left| {f(c) - f(1)} \right| < (1 - c)\left| {f'(c)} \right| \\
  2.\dfrac{{f(1) - f(c)}}{{1 - c}} = f'(c) \\
  3.\left| {f(c) + f(1)} \right| < (1 + c)\left| {f'(c)} \right| \\
  4.\left| {f(c) - f(1)} \right| < \left| {f'(c)} \right| \\
  $

Answer 1

Hint: We will use Lagrange’s mean value theorem which states that if a function is differentiable on (0,1) and continuous on [0,1]. Then, there exists a c such that
 $ f'(c) = \dfrac{{f(1) - f(c)}}{{1 - c}} $ where $ c \in (0,1) $ .
Now, using this theorem we will construct graphs and then interpret the values.

Complete step by step solution:
Case 1:
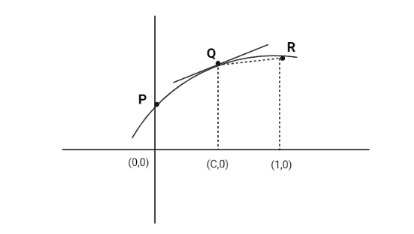
In the below image we see that,
 $ f'(c) > $ slope of $ QR $
Now, we know that slope of QR is $ \dfrac{{f(1) - f(c)}}{{1 - c}} $
Hence, $ f'(c) > \dfrac{{f(1) - f(c)}}{{1 - c}} $
 $ \therefore (1 - c)\left| {f'(c)} \right| > \left| {f(c) - f(1)} \right| $

Now, In the below figure we see that the slope of $ f'(c) $ and slope of QR is negative. But, the slope of $ f'(c) $ is more negative than the slope of QR.

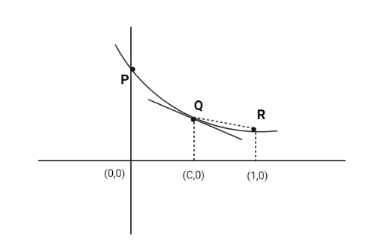
 $ \left| {f'(c)} \right| > $ | slope of QR|
we know that slope of QR is $ \dfrac{{f(1) - f(c)}}{{1 - c}} $
 $ \therefore (1 - c)\left| {f'(c)} \right| > \left| {f(c) - f(1)} \right| $
From the above two graphs we conclude that
 $ (1 - c)\left| {f'(c)} \right| > \left| {f(c) - f(1)} \right| $
Case 2:
In the below image we see that,

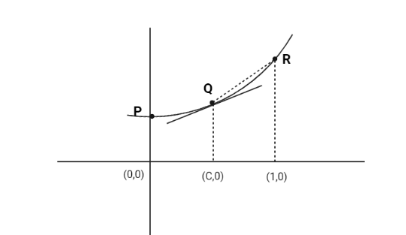
 $ f'(c) < $ slope of $ QR $
Now, we know that slope of QR is $ \dfrac{{f(1) - f(c)}}{{1 - c}} $
Hence, $ f'(c) < \dfrac{{f(1) - f(c)}}{{1 - c}} $
 $ \therefore (1 - c)\left| {f'(c)} \right| < \left| {f(c) - f(1)} \right| $
Now, In the below figure we see that the slope of $ f'(c) $ and slope of QR is negative. But, the slope of $ f'(c) $ is less negative than the slope of QR.

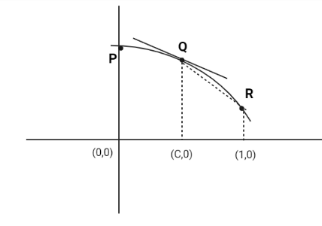
 $ \left| {f'(c)} \right| < $ | slope of QR|
we know that slope of QR is $ \dfrac{{f(1) - f(c)}}{{1 - c}} $
 $ \therefore (1 - c)\left| {f'(c)} \right| < \left| {f(c) - f(1)} \right| $
From the above two graphs we conclude that
 $ (1 - c)\left| {f'(c)} \right| < \left| {f(c) - f(1)} \right| $
Now, from all the available options we see that option 1 matches with case 2.
Hence the correct option is 1.
So, the correct answer is “Option 1”.

Note: In the proof of the Fundamental Theorem of Calculus, the Mean Value Theorem plays a significant part. If f exists and is bounded on the interior and is continuous on $ [a,b] $ , then f is of Bounded Variation on $ [a,b] $ .