Question

Let L denote the set of all straight lines in a plane. Let a relation R be defined by lRm, iff l is perpendicular to m for all \[l \in L\]. Then R is:
A) Reflexive
B) Symmetric
C) Transitive
D) None of these

Answer 1

Hint: We will first write the conditions for a relation to be reflexive, symmetric and transitive and then check the given relation, if it falls under any of the categories and we will get the answer.

Complete step-by-step answer:
Let us first of all see what it means for a relation to be:-
Reflexive:- A relation R on a set A is said to be reflexive iff aRa for all $a \in A$.
Symmetric:- A relation R on a set A is said to be symmetric if aRb implies bRa for all $a,b \in A$.
Transitive:- A relation R on a set A is said to be transitive if aRb and bRc implies that aRc for all $a,b,c \in A$.
Now, we will check for the given relation in question.
We are given that the set L consists of all the straight lines in a plane.
The relation R is defined by lRm iff l is perpendicular to m for all \[l \in L\].
Let us first check the reflexive property:-
If R is reflexive, then by the definition of reflexive, lRl for all $l \in L$.
But, one line can never be perpendicular to itself.
Hence, the relation R is not reflexive.
Let us now check the symmetric property:-
If R is symmetric, then by the definition of symmetric, if lRm then mRl for all $m,l \in L$.
If one line l is given perpendicular to some line m, then m will also be perpendicular to l as well.
Hence, the relation R is symmetric.
Let us now check the transitive property:-
If R is transitive, then by the definition of transitive, if lRm and mRn then lRm for all $l,m,n \in L$.
We will disprove this using an example:-

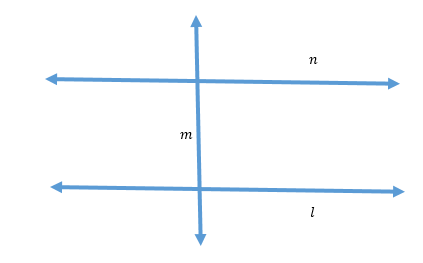
Here, we have l perpendicular to m and m is perpendicular to n.
But, l is not perpendicular to n.
Hence, the relation R is not transitive.

Hence, the correct option is (B).

Note: While checking the transitive portion, the students might make the mistake of thinking of the coordinate axis with x-axis, y-axis and z-axis in which all the axes are perpendicular to each other. But always remember that to prove something is true, you have to give a solid proof not an example and to prove something wrong, we just need an example to do so.
Consider if the question had the word “parallel” instead of the word “perpendicular” , the relation would have come to be equivalence relation because a line is always parallel to itself and if one line l is parallel to m and m is parallel to n, then I would be parallel to n and if one line is parallel to another, it applies vice-versa.