Question

Let $f:R\to R$ be denoted by $f\left( x \right)=\dfrac{x}{1+{{x}^{2}}},x\in R$. Then the range of f is :
A. $\left( -1,1 \right)-0$
B. $\left[ -\dfrac{1}{2},\dfrac{1}{2} \right]$
C. $R-\left[ -\dfrac{1}{2},\dfrac{1}{2} \right]$
D. $R-\left[ -1,1 \right]$

Answer 1

Hint: Here the given function maps from $R\to R$, so we will start solving the question by replacing $f\left( x \right)$ as $y$ and then we will use cross multiplication. With the cross multiplication, we will get a quadratic equation in $x$ and then when we put in $D={{b}^{2}}-4ac$ to check if it is greater than or equal to 0, we will get the range of the function.

Complete step-by-step answer:
In this question, we have a function which is rational and is in terms of $x$, that is, $f\left( x \right)=\dfrac{x}{1+{{x}^{2}}}$. It also has been mentioned that the domain of the function or we can say that the value of the $x$is that the function can take up is $R$, which means that on an infinite number line, $x$ can be anything. SO, we have to now find the range of the function, that is the values of $y$ or $f\left( x \right)$ that will come up limiting at various values of $x$. So, we start solving by making a quadratic equation in $x$ by replacing $f\left( x \right)$ as $y$ and use cross multiplication. So, doing so, we will get,
$\begin{align}
  & y=\dfrac{x}{1+{{x}^{2}}} \\
 & \Rightarrow y\left( 1+{{x}^{2}} \right)=x \\
 & \Rightarrow y+y{{x}^{2}}=x \\
 & \Rightarrow y{{x}^{2}}-x+y=0 \\
\end{align}$
So, now we will compare this quadratic equation with the general equation, that is, $a{{x}^{2}}+bx+c=0$, whose D is written as, $D={{b}^{2}}-4ac$. So, we have the value of D as,
$\begin{align}
  & D={{\left( -1 \right)}^{2}}-4\times y\times y \\
 & \Rightarrow D=1-4{{y}^{2}} \\
\end{align}$
Now, we will go to the next step of finding the range by putting the value of $D\ge 0$, so we will get,
$1-4{{y}^{2}}\ge 0$
$\Rightarrow \left( 1-2y \right)\left( 1+2y \right)\ge 0$, [As, we know that the identity ${{a}^{2}}-{{b}^{2}}=\left( a-b \right)\left( a+b \right)$]
So, we can see here that the critical points are $\dfrac{-1}{2}$ and $\dfrac{1}{2}$. The critical points mentioned implies those values where, $1-4{{y}^{2}}=0$. So, we will draw a number line and mark both the points and using the wavy curve concept, we will assign the sign convention.

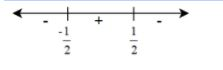
So, from this, we can see that the value of $y$ lies in the interval of $\left[ -\dfrac{1}{2},\dfrac{1}{2} \right]$. We have used [], that is closed brackets as we can see that there is an equality sign in the inequality equation.

So, the correct answer is “Option B”.

Note: Here in the solution, the use of brackets and wavy curve sign convention should be taken care of specifically. Be careful while choosing the options, as option C is similar, the only difference is that it is subtracted from $R$. It is not the correct answer but we have the interval between the points as $\dfrac{-1}{2}$ and $\dfrac{1}{2}$ and not beyond it, so be aware not to choose this option. The basic approach of solving these rational functions is the same, that is forming a quadratic equation in $x$ and then putting $D\ge 0$.