Question

Let $f\left( x \right)=\left\{ \begin{align}
  & -4;\text{ }-4 < x < 0 \\
 & {{x}^{2}}-4;\text{ }0\le x < 4 \\
\end{align} \right\}$. Discuss the continuity and differentiability of $g\left( x \right)=\left| f\left( x \right) \right|$ .
(a) Continuous everywhere but not differentiable at $x=2$.
(b) Continuous and differentiable at all the points.
(c) Not continuous and not differentiable at $x=2$.
(d) Continuous everywhere but not differentiable at $x=2,3$.

Answer 1

Hint: To find the continuity and differentiability for $g\left( x \right)=\left| f\left( x \right) \right|$, we are going to first of all draw the graph of the function $f\left( x \right)$. Then we are going to take the modulus of $f\left( x \right)$. When we take the modulus of $f\left( x \right)$, we are going to take the mirror image of the graph lying in the negative y-axis in the line mirror of x – axis. Now, to check the continuity of the function, if the function is not breaking at any point then it is a continuous function otherwise not and to check the differentiability of the function, if you see any sharp points in the curve then at that point the function is not differentiable.

Complete step-by-step solution:
In the above problem, we have given a function $f\left( x \right)$ as follows:
$f\left( x \right)=\left\{ \begin{align}
  & -4;\text{ }-4 < x < 0 \\
 & {{x}^{2}}-4;\text{ }0\le x < 4 \\
\end{align} \right\}$
Now, we are going to draw the above function as follows:

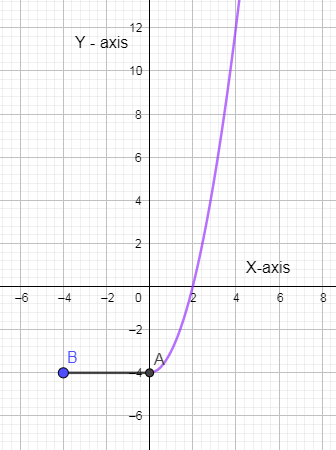
In the above graph, the purple-colored curve is when the x lies between 0 to 4 and the black solid line is when the graph lies between -4 to 0.
Now, we are going to take the modulus of the above graph which will then become the function $g\left( x \right)$. When we take the modulus of the above graph then we are going to take the image of the part of the curve which lies in the negative y-axis in the line mirror of x-axis. By taking this mirror image then the above graph will look like this:

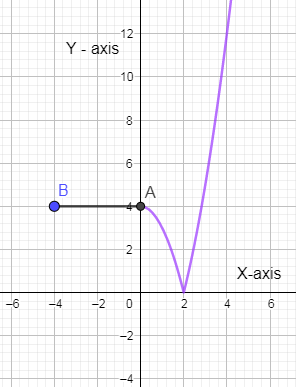
Now, as you can see that from the x – value of -4 to 4 there is no breakage of the curve. This means that the function $g\left( x \right)$ is a continuous function at all the points from -4 to 4. And to check the differentiability of the function $g\left( x \right)$ we are going to see whether we can see any sharp edge in the given curve. At point $x=2$, you can find the curve has a sharp edge so at $x=2$, the function $g\left( x \right)$ is not differentiable.
Hence, the correct option is (a).

Note: To solve the above function, you need to have a strong understanding of the continuity and differentiability of functions. Also, you should know how to see if a function in certain restrictions of the domain is continuous and differentiable. You also know how to calculate the modulus of a function so make sure you will properly learn these concepts.