
Let \[\alpha \], \[\beta \] and \[\gamma \] are the roots of \[{x^3} - 3{x^2} + 3x + 7 = 0\] (\[\omega \] is cube root of unity) then
\[\left( {\dfrac{{\alpha - 1}}{{\beta - 1}} + \dfrac{{\beta - 1}}{{\gamma - 1}} + \dfrac{{\gamma - 1}}{{\alpha - 1}}} \right)\]
A) \[\dfrac{3}{\omega }\]
B) \[{\omega ^2}\]
C) \[2{\omega ^2}\]
D) \[3{\omega ^2}\]
Answer
558.9k+ views
Hint:
Here, we will find the roots of the given equation using a long division method. Then, we will write those roots in the form of omega. Then, substituting the obtained values in the given sum of fractions will give us our required answer.
Formula Used:
We will use the following formulas:
1) Dividend \[ = \] Divisor \[ \times \] Quotient \[ + \] Remainder
2) \[x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}\], where \[a,b,c\]represents the coefficients of the quadratic equation \[a{x^2} + bx + c = 0\]
Complete step by step solution:
First of all, the given cubic polynomial is: \[{x^3} - 3{x^2} + 3x + 7 = 0\]
By hit and try method, let’s put \[x = - 1\] in the above equation. Therefore, we get
\[ - 1 - 3 - 3 + 7 = 0\]
\[ \Rightarrow 0 = 0\]
Hence, LHS \[ = \] RHS
Therefore, \[\left( {x + 1} \right)\] is the required divisor and it should divide the given cubic equation.
Thus, we will do long division:
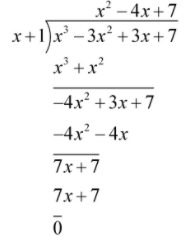
Hence, the quotient is \[{x^2} - 4x + 7\] and the remainder is 0.
Therefore, we can write this Dividend in the form of:
Dividend \[ = \]Divisor \[ \times \] Quotient \[ + \] Remainder
Substituting the values in the above equation, we get
\[ \Rightarrow {x^3} - 3{x^2} + 3x + 7 = \left( {x + 1} \right)\left( {{x^2} - 4x + 7} \right) + 0\]
Hence, \[x = - 1\]
Now, we will compare the quadratic equation in the RHS by the general form quadratic equation, i.e. \[a{x^2} + bx + c = 0\].
Now, using the quadratic formula, roots of the general equation are \[x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}\].
Here, substituting \[a = 1\], \[b = - 4\]and \[c = 7\]from the equation \[{x^2} - 4x + 7\]in the formula \[x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}\], we get the roots as:
\[x = \dfrac{{4 \pm \sqrt {{{\left( { - 4} \right)}^2} - 4\left( 1 \right)\left( 7 \right)} }}{{2\left( 1 \right)}}\]
Simplifying the expression, we get
\[ \Rightarrow x = \dfrac{{4 \pm \sqrt {16 - 28} }}{2}\]
Subtracting the terms, we get
\[\begin{array}{l} \Rightarrow x = \dfrac{{4 \pm \sqrt {12} }}{2}\\ \Rightarrow x = \dfrac{{4 \pm 2\sqrt {3i} }}{2}\end{array}\]
(We have taken iota \[\left( i \right)\] because there can’t be a negative number inside the square root, hence, this forms a complex or imaginary number.)
\[ \Rightarrow x = 2 \pm \sqrt {3i} \]
Hence, the three roots of the given equation \[{x^3} - 3{x^2} + 3x + 7 = 0\] are:
\[\alpha = - 1\], \[\beta = 2 + \sqrt {3i} \] and \[\gamma = 2 + \sqrt {3i} \]
Now, we know that \[\omega \]is cube root of unity
Hence, \[\alpha = - 1\], \[\beta = 1 - 2\omega \] and \[\gamma = 1 - 2{\omega ^2}\], where \[2\omega = - 1 + \sqrt 3 i\] and \[2{\omega ^2} = - 1 - \sqrt 3 i\]
Now, substituting them in \[\left( {\dfrac{{\alpha - 1}}{{\beta - 1}} + \dfrac{{\beta - 1}}{{\gamma - 1}} + \dfrac{{\gamma - 1}}{{\alpha - 1}}} \right)\], we get
\[\left( {\dfrac{{\alpha - 1}}{{\beta - 1}} + \dfrac{{\beta - 1}}{{\gamma - 1}} + \dfrac{{\gamma - 1}}{{\alpha - 1}}} \right) = \left( {\dfrac{{ - 1 - 1}}{{1 - 2\omega - 1}} + \dfrac{{1 - 2\omega - 1}}{{1 - 2{\omega ^2} - 1}} + \dfrac{{1 - 2{\omega ^2} - 1}}{{ - 1 - 1}}} \right)\]
Adding and subtracting the like terms, we get
\[ \Rightarrow \left( {\dfrac{{\alpha - 1}}{{\beta - 1}} + \dfrac{{\beta - 1}}{{\gamma - 1}} + \dfrac{{\gamma - 1}}{{\alpha - 1}}} \right) = \left( {\dfrac{{ - 2}}{{ - 2\omega }} + \dfrac{{ - 2\omega }}{{ - 2{\omega ^2}}} + \dfrac{{ - 2{\omega ^2}}}{{ - 2}}} \right)\]
Simplifying the expression, we get
\[ \Rightarrow \left( {\dfrac{{\alpha - 1}}{{\beta - 1}} + \dfrac{{\beta - 1}}{{\gamma - 1}} + \dfrac{{\gamma - 1}}{{\alpha - 1}}} \right) = \left( {\dfrac{1}{\omega } + \dfrac{1}{\omega } + {\omega ^2}} \right) = \left( {\dfrac{2}{\omega } + {\omega ^2}} \right)\]
Hence, this can also be written as:
\[ \Rightarrow \left( {\dfrac{{\alpha - 1}}{{\beta - 1}} + \dfrac{{\beta - 1}}{{\gamma - 1}} + \dfrac{{\gamma - 1}}{{\alpha - 1}}} \right) = \left( {2{\omega ^2} + {\omega ^2}} \right) = 3{\omega ^2}\]
(This is because, if we substitute the value of omega, then, we get the overall value as the value of \[2{\omega ^2}\])
Therefore, the value of \[\left( {\dfrac{{\alpha - 1}}{{\beta - 1}} + \dfrac{{\beta - 1}}{{\gamma - 1}} + \dfrac{{\gamma - 1}}{{\alpha - 1}}} \right) = 3{\omega ^2}\]
Hence, option D is the correct answer.
Note:
Let us assume the cube root of unity or 1 as:
\[\sqrt[3]{1} = z\]
Cubing both sides,
\[ \Rightarrow 1 = {z^3}\]
Or
\[ \Rightarrow {z^3} - 1 = 0\]
Now, using the formula \[\left( {{a^3} - {b^3}} \right) = \left( {a - b} \right)\left( {{a^2} + {b^2} + ab} \right)\]
\[ \Rightarrow \left( {z - 1} \right)\left( {{z^2} + z + 1} \right) = 0\]
Therefore, either \[\left( {z - 1} \right) = 0\]
\[ \Rightarrow z = 1\]
Or, \[\left( {{z^2} + z + 1} \right) = 0\]
Comparing with \[\left( {a{x^2} + bx + c} \right) = 0\]
Here, \[a = 1\], \[b = 1\] and \[c = 1\]
Now, Determinant, \[D = {b^2} - 4ac\]
Hence, for \[\left( {{z^2} + z + 1} \right) = 0\],
\[D = {\left( 1 \right)^2} - 4 \times 1 = 1 - 4 = - 3\]
Now, , Using quadratic formula,
\[z = \dfrac{{ - b \pm \sqrt D }}{{2a}}\]
Here, \[a = 1\], \[b = 1\]and \[c = 1\] and \[D = - 3\]
\[ \Rightarrow z = \dfrac{{ - 1 \pm \sqrt { - 3} }}{2}\]
This can be written as:
\[ \Rightarrow z = \dfrac{{ - 1 \pm \sqrt 3 i}}{2}\]
Therefore, the three cube roots of unity are:
\[1\], \[\dfrac{{ - 1}}{2} + \dfrac{{\sqrt 3 i}}{2}\] and \[\dfrac{{ - 1}}{2} - \dfrac{{\sqrt 3 i}}{2}\]
Now, according to the property, the sum of these three cube roots of unity will be equal to 0.
We know that,
\[1 + \omega + {\omega ^2} = 0\]
Here, \[\omega \]represents the imaginary cube roots.
\[ \Rightarrow 1 + \dfrac{{ - 1}}{2} + \dfrac{{\sqrt 3 i}}{2} + \dfrac{{ - 1}}{2} - \dfrac{{\sqrt 3 i}}{2} = 1 - 1 + 0 = 0\]
Hence, proved
Therefore, due to this property; in this question we have assumed the values of our roots in the form of omega.
Here, we will find the roots of the given equation using a long division method. Then, we will write those roots in the form of omega. Then, substituting the obtained values in the given sum of fractions will give us our required answer.
Formula Used:
We will use the following formulas:
1) Dividend \[ = \] Divisor \[ \times \] Quotient \[ + \] Remainder
2) \[x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}\], where \[a,b,c\]represents the coefficients of the quadratic equation \[a{x^2} + bx + c = 0\]
Complete step by step solution:
First of all, the given cubic polynomial is: \[{x^3} - 3{x^2} + 3x + 7 = 0\]
By hit and try method, let’s put \[x = - 1\] in the above equation. Therefore, we get
\[ - 1 - 3 - 3 + 7 = 0\]
\[ \Rightarrow 0 = 0\]
Hence, LHS \[ = \] RHS
Therefore, \[\left( {x + 1} \right)\] is the required divisor and it should divide the given cubic equation.
Thus, we will do long division:
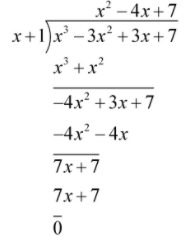
Hence, the quotient is \[{x^2} - 4x + 7\] and the remainder is 0.
Therefore, we can write this Dividend in the form of:
Dividend \[ = \]Divisor \[ \times \] Quotient \[ + \] Remainder
Substituting the values in the above equation, we get
\[ \Rightarrow {x^3} - 3{x^2} + 3x + 7 = \left( {x + 1} \right)\left( {{x^2} - 4x + 7} \right) + 0\]
Hence, \[x = - 1\]
Now, we will compare the quadratic equation in the RHS by the general form quadratic equation, i.e. \[a{x^2} + bx + c = 0\].
Now, using the quadratic formula, roots of the general equation are \[x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}\].
Here, substituting \[a = 1\], \[b = - 4\]and \[c = 7\]from the equation \[{x^2} - 4x + 7\]in the formula \[x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}\], we get the roots as:
\[x = \dfrac{{4 \pm \sqrt {{{\left( { - 4} \right)}^2} - 4\left( 1 \right)\left( 7 \right)} }}{{2\left( 1 \right)}}\]
Simplifying the expression, we get
\[ \Rightarrow x = \dfrac{{4 \pm \sqrt {16 - 28} }}{2}\]
Subtracting the terms, we get
\[\begin{array}{l} \Rightarrow x = \dfrac{{4 \pm \sqrt {12} }}{2}\\ \Rightarrow x = \dfrac{{4 \pm 2\sqrt {3i} }}{2}\end{array}\]
(We have taken iota \[\left( i \right)\] because there can’t be a negative number inside the square root, hence, this forms a complex or imaginary number.)
\[ \Rightarrow x = 2 \pm \sqrt {3i} \]
Hence, the three roots of the given equation \[{x^3} - 3{x^2} + 3x + 7 = 0\] are:
\[\alpha = - 1\], \[\beta = 2 + \sqrt {3i} \] and \[\gamma = 2 + \sqrt {3i} \]
Now, we know that \[\omega \]is cube root of unity
Hence, \[\alpha = - 1\], \[\beta = 1 - 2\omega \] and \[\gamma = 1 - 2{\omega ^2}\], where \[2\omega = - 1 + \sqrt 3 i\] and \[2{\omega ^2} = - 1 - \sqrt 3 i\]
Now, substituting them in \[\left( {\dfrac{{\alpha - 1}}{{\beta - 1}} + \dfrac{{\beta - 1}}{{\gamma - 1}} + \dfrac{{\gamma - 1}}{{\alpha - 1}}} \right)\], we get
\[\left( {\dfrac{{\alpha - 1}}{{\beta - 1}} + \dfrac{{\beta - 1}}{{\gamma - 1}} + \dfrac{{\gamma - 1}}{{\alpha - 1}}} \right) = \left( {\dfrac{{ - 1 - 1}}{{1 - 2\omega - 1}} + \dfrac{{1 - 2\omega - 1}}{{1 - 2{\omega ^2} - 1}} + \dfrac{{1 - 2{\omega ^2} - 1}}{{ - 1 - 1}}} \right)\]
Adding and subtracting the like terms, we get
\[ \Rightarrow \left( {\dfrac{{\alpha - 1}}{{\beta - 1}} + \dfrac{{\beta - 1}}{{\gamma - 1}} + \dfrac{{\gamma - 1}}{{\alpha - 1}}} \right) = \left( {\dfrac{{ - 2}}{{ - 2\omega }} + \dfrac{{ - 2\omega }}{{ - 2{\omega ^2}}} + \dfrac{{ - 2{\omega ^2}}}{{ - 2}}} \right)\]
Simplifying the expression, we get
\[ \Rightarrow \left( {\dfrac{{\alpha - 1}}{{\beta - 1}} + \dfrac{{\beta - 1}}{{\gamma - 1}} + \dfrac{{\gamma - 1}}{{\alpha - 1}}} \right) = \left( {\dfrac{1}{\omega } + \dfrac{1}{\omega } + {\omega ^2}} \right) = \left( {\dfrac{2}{\omega } + {\omega ^2}} \right)\]
Hence, this can also be written as:
\[ \Rightarrow \left( {\dfrac{{\alpha - 1}}{{\beta - 1}} + \dfrac{{\beta - 1}}{{\gamma - 1}} + \dfrac{{\gamma - 1}}{{\alpha - 1}}} \right) = \left( {2{\omega ^2} + {\omega ^2}} \right) = 3{\omega ^2}\]
(This is because, if we substitute the value of omega, then, we get the overall value as the value of \[2{\omega ^2}\])
Therefore, the value of \[\left( {\dfrac{{\alpha - 1}}{{\beta - 1}} + \dfrac{{\beta - 1}}{{\gamma - 1}} + \dfrac{{\gamma - 1}}{{\alpha - 1}}} \right) = 3{\omega ^2}\]
Hence, option D is the correct answer.
Note:
Let us assume the cube root of unity or 1 as:
\[\sqrt[3]{1} = z\]
Cubing both sides,
\[ \Rightarrow 1 = {z^3}\]
Or
\[ \Rightarrow {z^3} - 1 = 0\]
Now, using the formula \[\left( {{a^3} - {b^3}} \right) = \left( {a - b} \right)\left( {{a^2} + {b^2} + ab} \right)\]
\[ \Rightarrow \left( {z - 1} \right)\left( {{z^2} + z + 1} \right) = 0\]
Therefore, either \[\left( {z - 1} \right) = 0\]
\[ \Rightarrow z = 1\]
Or, \[\left( {{z^2} + z + 1} \right) = 0\]
Comparing with \[\left( {a{x^2} + bx + c} \right) = 0\]
Here, \[a = 1\], \[b = 1\] and \[c = 1\]
Now, Determinant, \[D = {b^2} - 4ac\]
Hence, for \[\left( {{z^2} + z + 1} \right) = 0\],
\[D = {\left( 1 \right)^2} - 4 \times 1 = 1 - 4 = - 3\]
Now, , Using quadratic formula,
\[z = \dfrac{{ - b \pm \sqrt D }}{{2a}}\]
Here, \[a = 1\], \[b = 1\]and \[c = 1\] and \[D = - 3\]
\[ \Rightarrow z = \dfrac{{ - 1 \pm \sqrt { - 3} }}{2}\]
This can be written as:
\[ \Rightarrow z = \dfrac{{ - 1 \pm \sqrt 3 i}}{2}\]
Therefore, the three cube roots of unity are:
\[1\], \[\dfrac{{ - 1}}{2} + \dfrac{{\sqrt 3 i}}{2}\] and \[\dfrac{{ - 1}}{2} - \dfrac{{\sqrt 3 i}}{2}\]
Now, according to the property, the sum of these three cube roots of unity will be equal to 0.
We know that,
\[1 + \omega + {\omega ^2} = 0\]
Here, \[\omega \]represents the imaginary cube roots.
\[ \Rightarrow 1 + \dfrac{{ - 1}}{2} + \dfrac{{\sqrt 3 i}}{2} + \dfrac{{ - 1}}{2} - \dfrac{{\sqrt 3 i}}{2} = 1 - 1 + 0 = 0\]
Hence, proved
Therefore, due to this property; in this question we have assumed the values of our roots in the form of omega.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




