Question

Let ABC be an equilateral triangle with side length $a$. Let $R$ and $r$ denote the radii of the circumcircle and the incircle of triangle ABC respectively. Then, as a function of $a$, the ratio $\dfrac{R}{r}$
(a) Strictly increases
(b) Strictly decreases
(c) Remains constant
(d) Strictly increases for $a < 1$ and strictly decreases for $a > 1$

Answer 1

Hint: We will draw a rough diagram representing the equilateral triangle, the circumcircle and the incircle. We will see that the radii of the circumcircle and the incircle together form the altitude of the equilateral triangle. We will find the length of the altitude in terms of the side length using the trigonometric ratios of a $30{}^\circ \text{-}60{}^\circ \text{-}90{}^\circ $ triangle. Then we will use the property of the centroid of the equilateral triangle to find the trend of the ratio of the two radii.

Complete step by step answer:
The rough diagram of the equilateral triangle with its circumcircle and incircle looks like the following,

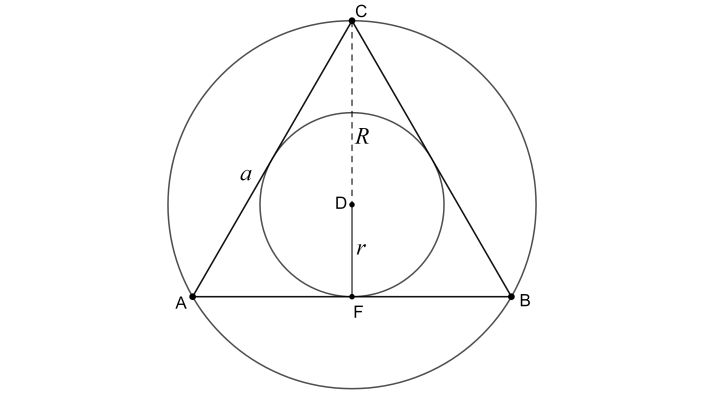
From the diagram, we can see that segment CD is the radius of the circumcircle and segment DF is the radius of the incircle. Also, segment CF is the altitude of the equilateral triangle from vertex A. Each angle of an equilateral triangle is $60{}^\circ $. Now, we know that $\sin 60{}^\circ =\dfrac{\sqrt{3}}{2}$ and $\sin \theta =\dfrac{\text{Opposite}}{\text{Hypotenuse}}$. So, in $\Delta \text{CAF}$, we have the following,
$\begin{align}
  & \sin A=\dfrac{\text{CF}}{\text{AC}} \\
 & \Rightarrow \sin 60{}^\circ =\dfrac{\text{CF}}{a} \\
 & \Rightarrow \dfrac{\sqrt{3}}{2}=\dfrac{\text{CF}}{a} \\
 & \therefore \text{CF}=\dfrac{\sqrt{3}}{2}a \\
\end{align}$
From the figure, we can see that $\text{CF}=\text{CD}+\text{DF}$. Now, we have a property that the centroid of an equilateral triangle coincides with the centre of the circumcircle as well as the incircle. Also, we know that the centroid of an equilateral triangle divides the median into the ratio $1:2$ and in an equilateral triangle, the median, altitude and angle bisector drawn from the same vertex coincide.
Hence, we have the following,
$\begin{align}
  & \text{CD}=\dfrac{2}{3}\text{CF} \\
 & \Rightarrow \text{CD}=\dfrac{2}{3}\times \dfrac{\sqrt{3}}{2}a \\
 & \therefore \text{CD}=\dfrac{1}{\sqrt{3}}a \\
\end{align}$
In a similar way, we have
$\begin{align}
  & \text{DF}=\dfrac{1}{3}\text{CF} \\
 & \Rightarrow \text{DF}=\dfrac{1}{3}\times \dfrac{\sqrt{3}}{2}a \\
 & \therefore \text{DF}=\dfrac{1}{2\sqrt{3}}a \\
\end{align}$
Therefore, we have $R=\dfrac{1}{\sqrt{3}}a$ and $r=\dfrac{1}{2\sqrt{3}}a$. Now, looking at the ratio, we get
$\begin{align}
  & \dfrac{R}{r}=\dfrac{\left( \dfrac{1}{\sqrt{3}}a \right)}{\left( \dfrac{1}{2\sqrt{3}}a \right)} \\
 & \Rightarrow \dfrac{R}{r}=\dfrac{a}{\sqrt{3}}\times \dfrac{2\sqrt{3}}{a} \\
 & \therefore \dfrac{R}{r}=2 \\
\end{align}$
Hence, the ratio of the radii does not depend on the side length of the equilateral triangle and remains constant.

So, the correct answer is “Option c”.

Note: We should be familiar with the geometric properties of the equilateral triangle. These properties are useful in solving such types of questions. It is beneficial to make a rough diagram so that the properties and relations between different segments are visible. It is also useful to know the trigonometric ratios of standard angles.