Question

Let AB be a sector of a circle with centre O and radius d. $\angle \text{AOB = }\theta \left( <\dfrac{\pi }{2} \right)$, and D be a point on OA such that BD is perpendicular to OA. Let E be the midpoint of BD and F be a point on the arc AB such that EF is parallel to OA. Then the ratio of length of the arc AF to the length of the arc AB is?
(a) $\dfrac{1}{2}$
(b) $\dfrac{\theta }{2}$
(c) $\dfrac{1}{2}\sin \theta $
(d) ${{\sin }^{-1}}\left( \dfrac{1}{2}\sin \theta \right)$

Answer 1

Hint: We will construct a diagram using the given information. We will find the ratio of the arc lengths using the formula for calculating the arc length. Then, we will obtain that ratio in terms of angles. From the figure, we will be able to look at two similar triangles. Using these triangles and the trigonometric ratios of the required angles, we will be able to obtain the correct answer.

Complete step-by-step answer:
Let us draw a figure that represents all the given information. We will join the segment OF as well. Let us assume that $\angle \text{AOF = }\alpha $. The figure looks like the following,

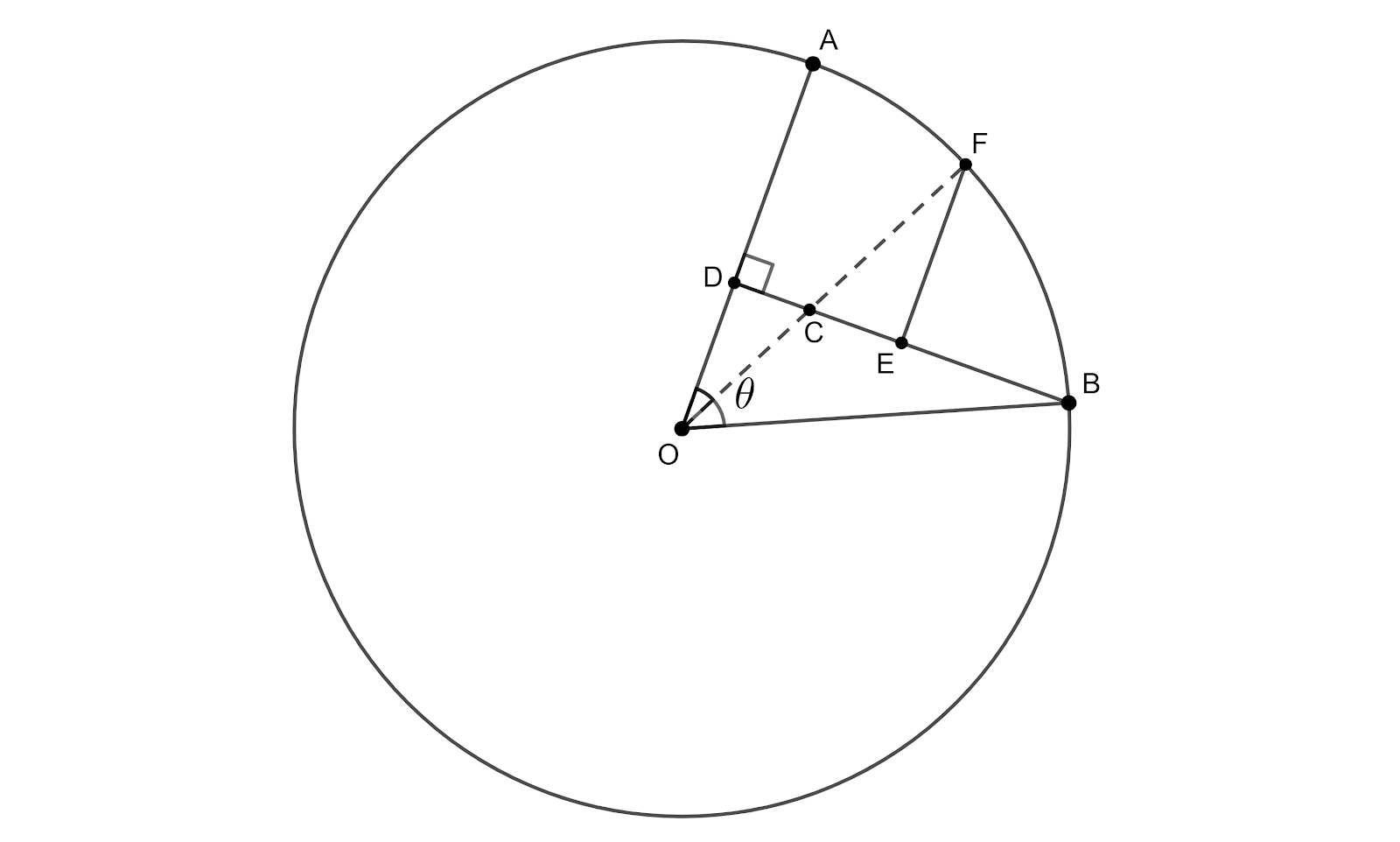
We have to find the ratio $\dfrac{l\left( \text{AF} \right)}{l\left( \text{AB} \right)}$. We know that the length of the arc of a circle is given as $s=r\theta $ where $s$ is the arc length, $r$ is the radius of the circle and $\theta $ is the central angle. Therefore, we get
$\dfrac{l\left( \text{AF} \right)}{l\left( \text{AB} \right)}=\dfrac{d\cdot \alpha }{d\cdot \theta }=\dfrac{\alpha }{\theta }$
From the figure, we can see that $\Delta \text{DOC}$ and $\Delta \text{EFC}$ are right angled triangles. We can see that $\angle \text{ODC = }\angle \text{FEC = 90}{}^\circ $ and $\angle \text{DOC = }\angle \text{EFC = }\alpha $ since they are alternate angles. So, these two triangles are similar. Now, we know that $\sin \theta =\dfrac{\text{Opposite}}{\text{Hypotenuse}}$. So, in $\Delta \text{BDO}$, $\sin \theta =\dfrac{\text{BD}}{\text{OB}}$. This implies that $\text{BD}\text{ = }d\sin \theta $. Since, E is the midpoint of BD, we get $\text{ED = }\dfrac{1}{2}d\sin \theta $.
Let us consider the following expression,
$\text{OC}\left( \sin \alpha \right)+\text{CF}\left( \sin \alpha \right)$
In the first term of the above expression, $\sin \alpha =\dfrac{\text{CD}}{\text{OC}}$. And in the second term, $\sin \alpha =\dfrac{\text{CE}}{\text{CF}}$. So, we have the following,
$\begin{align}
  & \text{OC}\left( \sin \alpha \right)+\text{CF}\left( \sin \alpha \right)=\text{OC }\dfrac{\text{CD}}{\text{OC}}+\text{CF }\dfrac{\text{CE}}{\text{CF}} \\
 & \Rightarrow \text{OC}\left( \sin \alpha \right)+\text{CF}\left( \sin \alpha \right)=\text{CD}+\text{CE} \\
 & \therefore \text{OC}\left( \sin \alpha \right)+\text{CF}\left( \sin \alpha \right)=\text{ED} \\
\end{align}$
In the above expression, we can write $\text{CF = }d-\text{OC}$ and $\text{ED = }\dfrac{1}{2}d\sin \theta $. Substituting these values, we get
$\begin{align}
  & \text{OC}\left( \sin \alpha \right)+\left( d-\text{OC} \right)\left( \sin \alpha \right)=\dfrac{1}{2}d\sin \theta \\
 & \Rightarrow d\sin \alpha =\dfrac{1}{2}d\sin \theta \\
 & \Rightarrow \sin \alpha =\dfrac{1}{2}\sin \theta \\
 & \therefore \alpha ={{\sin }^{-1}}\left( \dfrac{1}{2}\sin \theta \right) \\
\end{align}$

So, the correct answer is “Option (d)”.

Note: It is important that we construct the figure as accurately as possible. Looking at the figure helps us realize useful facts, for example $\text{CD}+\text{CE=ED}$. Understanding the geometric construction of a figure is the key aspect in this type of questions. We should be familiar with the trigonometric ratios of an angle in a triangle.