Question

Let ${{A}_{0}},{{A}_{1}},{{A}_{2}},{{A}_{3}},{{A}_{4}}\text{ and }{{A}_{5}}$ be a vertex of regular hexagon inscribed in a circle of unit radius. Then the product of the length of the line segment ${{A}_{0}}{{A}_{1}},{{A}_{0}}{{A}_{2}}\text{ and }{{A}_{0}}{{A}_{4}}$ is
\[\begin{align}
  & A.\dfrac{3}{4} \\
 & B.3\sqrt{3} \\
 & C.3 \\
 & D.\dfrac{3\sqrt{3}}{2} \\
\end{align}\]

Answer 1

Hint: We are given that, we have a unit circle with a circle inscribed in a hexagon. Circle is of unit radius. We have to find length of ${{A}_{0}},{{A}_{1}},{{A}_{2}},{{A}_{3}},{{A}_{4}}\text{ and }{{A}_{5}}$. To do so we will use the circle to find the coordinate of those vertices, we use that hexagon subtend ${{60}^{\circ }}$ at the center from each side. Once we have coordinates, we will use $\cos {{60}^{\circ }}=\dfrac{1}{{2}}\text{ and }\sin {{60}^{\circ }}=\dfrac{\sqrt{3}}{2}$ and lastly we need distance formula $\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$ to find distance. Then, at last we will find the product.

Complete step-by-step solution:
We are given that ${{A}_{0}},{{A}_{1}},{{A}_{2}},{{A}_{3}},{{A}_{4}}\text{ and }{{A}_{5}}$ are vertex of a regular hexagon that is inscribed in a circle.
Let the circle have O as center. As we are given, the circle has unit radius, so we have $O{{A}_{0}}=1$.
$O{{A}_{0}}$ is radius as ${{A}_{0}}$ lies on the circle and O is the center.
So as ${{A}_{1}},{{A}_{2}},{{A}_{3}},{{A}_{4}}\text{ and }{{A}_{5}}$ also lies on circle. So, $O{{A}_{1}},O{{A}_{2}},O{{A}_{3}},O{{A}_{4}}\text{ and O}{{A}_{5}}$ are also radius. Hence,
$O{{A}_{1}}=O{{A}_{2}}=O{{A}_{3}}=O{{A}_{4}}=\text{O}{{A}_{5}}=1$.

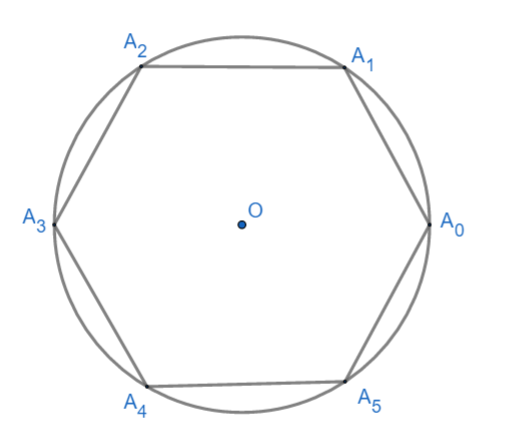
Now we know regular hexagon has each side equal and angle subtended by them at the center is of ${{60}^{\circ }}$ so,

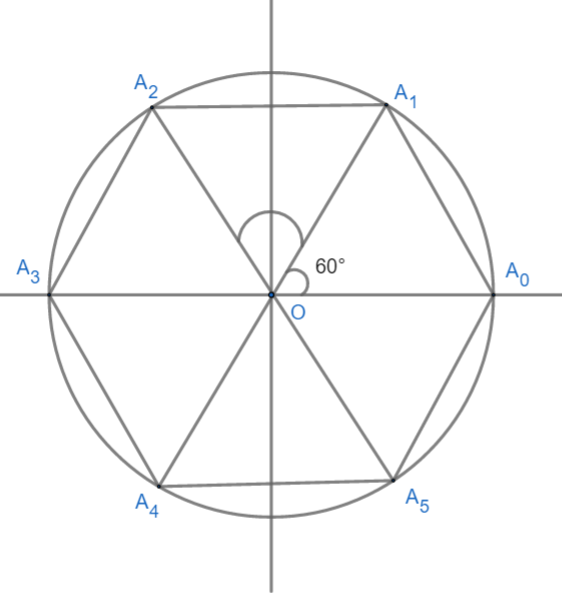
Now we will have to find the coordinate of the vertex of the hexagon.
As we have to find distance of ${{A}_{0}}{{A}_{1}},{{A}_{0}}{{A}_{2}}\text{ and }{{A}_{0}}{{A}_{4}}$ so we need coordinate of ${{A}_{0}},{{A}_{1}},{{A}_{2}}\text{ and }{{A}_{4}}$.
As angle subtends by each side, so we can see that, ${{A}_{0}}=\left( 1,0 \right)$ (as radius of circle is 1).
Now, coordinate of ${{A}_{1}}=\left( \cos {{60}^{\circ }},\sin {{60}^{\circ }} \right)$.
Similarly, we have ${{A}_{2}}=\left( \cos {{120}^{\circ }},\sin {{120}^{\circ }} \right)$.
Similarly, we have ${{A}_{4}}=\left( \cos {{240}^{\circ }},\sin {{240}^{\circ }} \right)$.
Now simplifying we get,
$\begin{align}
  & {{A}_{1}}=\left( \cos {{60}^{\circ }},\sin {{60}^{\circ }} \right)={{A}_{1}}\left( \dfrac{1}{2},\dfrac{\sqrt{3}}{2} \right) \\
 & {{A}_{2}}=\left( \cos {{120}^{\circ }},\sin {{120}^{\circ }} \right)={{A}_{2}}\left( \dfrac{-1}{2},\dfrac{\sqrt{3}}{2} \right) \\
\end{align}$
We can write it as we know that $\cos {{120}^{\circ }}=\cos \left( {{180}^{\circ }}-{{60}^{\circ }} \right)=-\cos {{60}^{\circ }}=-\dfrac{1}{2}$ and $\sin {{120}^{\circ }}=\sin \left( {{180}^{\circ }}-{{60}^{\circ }} \right)=\sin {{60}^{\circ }}=\dfrac{\sqrt{3}}{2}$.
${{A}_{4}}=\left( \cos {{240}^{\circ }},\sin {{240}^{\circ }} \right)=\left( -\dfrac{1}{2},\dfrac{-\sqrt{3}}{2} \right)$.
We can write it as we know that $\cos {{240}^{\circ }}=\cos \left( {{180}^{\circ }}+{{60}^{\circ }} \right)=-\cos {{60}^{\circ }}=-\dfrac{1}{2}$ and $\sin {{240}^{\circ }}=\sin \left( {{180}^{\circ }}+{{60}^{\circ }} \right)=-\sin {{60}^{\circ }}=\dfrac{-\sqrt{3}}{2}$.
Now we will find the distance, we know that for points \[A\left( {{x}_{1}},{{y}_{1}} \right)\text{ and }B\left( {{x}_{2}},{{y}_{2}} \right)\], the distance AB is given as $AB=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$.
So for
\[\begin{align}
  & {{A}_{0}}\left( 1,0 \right)\text{ and }{{A}_{1}}\left( \dfrac{1}{2},\dfrac{\sqrt{3}}{2} \right) \\
 & {{A}_{0}}{{A}_{1}}=\sqrt{{{\left( \dfrac{1}{2}-1 \right)}^{2}}+{{\left( \dfrac{\sqrt{3}}{2}-0 \right)}^{2}}} \\
\end{align}\].
Simplifying we get \[{{A}_{0}}{{A}_{1}}=\sqrt{{{\left( -\dfrac{1}{2} \right)}^{2}}+{{\left( \dfrac{\sqrt{3}}{2} \right)}^{2}}}=\sqrt{\dfrac{4}{4}}=1\].
Similarly, for
\[\begin{align}
  & {{A}_{0}}\left( 1,0 \right)\text{ and }{{A}_{2}}\left( \dfrac{-1}{2},\dfrac{\sqrt{3}}{2} \right) \\
 & {{A}_{0}}{{A}_{2}}=\sqrt{{{\left( \dfrac{-1}{2}-1 \right)}^{2}}+{{\left( \dfrac{\sqrt{3}}{2}-0 \right)}^{2}}} \\
\end{align}\]
Simplifying we get \[{{A}_{0}}{{A}_{2}}=\sqrt{{{\left( -\dfrac{3}{2} \right)}^{2}}+{{\left( \dfrac{\sqrt{3}}{2} \right)}^{2}}}=\sqrt{\dfrac{9}{4}+\dfrac{3}{4}}=\sqrt{\dfrac{12}{4}}=\sqrt{3}\].
Now for
\[\begin{align}
  & {{A}_{0}}\left( 1,0 \right)\text{ and }{{A}_{4}}\left( \dfrac{-1}{2},\dfrac{-\sqrt{3}}{2} \right) \\
 & {{A}_{0}}{{A}_{2}}=\sqrt{{{\left( \dfrac{-1}{2}-1 \right)}^{2}}+{{\left( \dfrac{-\sqrt{3}}{2}-0 \right)}^{2}}} \\
\end{align}\]
Simplifying we get, \[{{A}_{0}}{{A}_{4}}=\sqrt{{{\left( -\dfrac{3}{2} \right)}^{2}}+{{\left( \dfrac{-\sqrt{3}}{2} \right)}^{2}}}\].
Solving we get, \[{{A}_{0}}{{A}_{4}}=\sqrt{\dfrac{9}{4}+\dfrac{3}{4}}=\sqrt{\dfrac{12}{4}}=\sqrt{3}\].
So we get \[{{A}_{0}}{{A}_{4}}=\sqrt{3}\].
Now, we are asked to find the product of ${{A}_{0}}{{A}_{1}},{{A}_{0}}{{A}_{2}}\text{ and }{{A}_{0}}{{A}_{4}}$. So, ${{A}_{0}}{{A}_{1}}\times {{A}_{0}}{{A}_{2}}\times {{A}_{0}}{{A}_{4}}=1\times \sqrt{3}\times \sqrt{3}=3$.
So the required product is 3.
Hence option C is the correct answer.

Note: While solving distance we need to be much focused. As mistakes like ${{\left( \dfrac{-3}{2} \right)}^{2}}=\dfrac{-9}{4},\dfrac{-1}{2}-1=\dfrac{-2}{2}$ may happen. Students must remember that, while doing square, sign always comes out as positive and for addition of fraction, we take LCM before adding.