Question

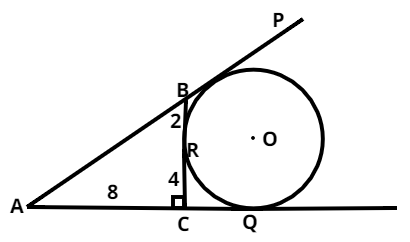
What is the length of AQ in the given figure?

Answer 1

Hint: Write AQ as $AC + CQ$. We know the value of AC and CR. So, use the property of tangent drawn from any external point to find the value of CQ.

Complete step-by-step answer:

As it is shown in the above figure that,
$ \Rightarrow AC = 8cm,{\text{ }}CR = 4cm{\text{ }}and{\text{ }}BR = 2cm$

Now, we had to find the length of AQ.

As, we see from the above figure that,
$ \Rightarrow AQ = AC + CQ$ (1)

And the length of AC is given,
And, as we know that the length of two tangents drawn from any external point of a circle to the circle has equal lengths.

$ \Rightarrow $So, length of CQ $ = $ length of CR
$ \Rightarrow $Length of CR $ = $4cm (given)
$ \Rightarrow $Hence, the length of CQ will be 4 cm.
So, putting the value of CQ and AC in equation 1. We get,
$ \Rightarrow AQ = AC + CQ{\text{ }} = 8 + 4 = 12$
$ \Rightarrow $ Hence, the length of AQ will be 12cm.

Note: Whenever we come up with this type of problem then the easiest and efficient way is to go with the property of tangents and circles. Because in most of the cases we can get the required answer from property only, without any calculations involved.