Question

It is known to all of you that the impedance of a circuit is dependent on the frequency of source. In order to study the effect of frequency on the impedance, a student in a lab took 2 impedance boxes P and Q and connected them in series with an AC source of variable frequency. The emf of the source is constant at 10V. Box P contains a capacitance of $1\mu F$in series with a resistance of $32\Omega $. And the box Q has a coil of self-inductance 4.9mH and a resistance of $68\Omega $in series. He adjusted the frequency so that the maximum current flows in P and Q. Based on his experimental setup and the reading by him at various moments, answer the following questions. Impedance of box P at the above frequency is
A. $70\Omega $
B. $77\Omega $
C. $90\Omega $
D. $100\Omega $

Answer 1

Hint: As a first step, one could read the question well and hence note down the important points from the question. Using that you could make a neat circuit diagram for better clarity. Then consider just the box only. Find the resonant frequency then the capacitive reactance and hence the impedance.
Formula used:
Resonant frequency,
$\omega =\dfrac{1}{\sqrt{LC}}$
Capacitive reactance,
${{X}_{C}}=\dfrac{1}{\omega C}$
Impedance,
$Z=\sqrt{{{R}_{1}}^{2}+{{X}_{C}}^{2}}$

Complete step by step answer:
From the description given in the question, one could make a circuit diagram as given below.

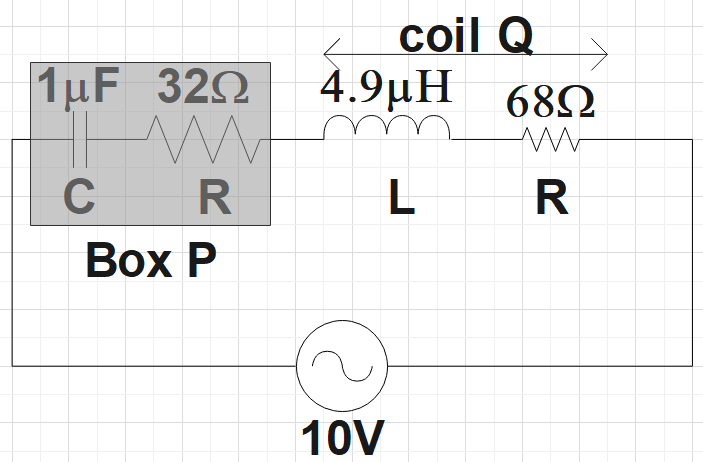
As a first step, let us find the resonant frequency using the following formula,
$\omega =\dfrac{1}{\sqrt{LC}}$
Substituting the given values, we get,
$\omega =\dfrac{1}{\sqrt{4.9\times {{10}^{-3}}\times {{10}^{-6}}}}=\dfrac{{{10}^{5}}}{7}rad/s$……………………………… (1)
Now consider the box P, we have a capacitor and resistor connected in series and the capacitive reactance would be,
${{X}_{C}}=\dfrac{1}{\omega C}=\dfrac{1}{\left( \dfrac{{{10}^{5}}}{7} \right)\times {{10}^{-6}}}=70\Omega $……………………………….. (2)
Now we could find the impedance of the box P as,
$Z=\sqrt{{{R}_{1}}^{2}+{{X}_{C}}^{2}}$
$\Rightarrow Z=\sqrt{{{32}^{2}}+{{70}^{2}}}$
$\therefore Z\approx 77\Omega $
Therefore, we found the impedance of the box P to be equal to $77\Omega $.

So, the correct answer is “Option B”.

Note: Though the question is one whole paragraph, this is a pretty basic question. We just have to filter out the required points from the question. Actually, the step where we made the circuit using the given information has given better clarity of the situation. Thus always try to make a rough sketch of the circuits whenever necessary.