Question

It is given that PQR is a right-angled triangle, right angled at Q, with sides PQ = 12 cm, QR = 9 cm and RP = 15 cm. If it is revolved about the side QR a solid right circular cone is obtained. Find the volume of this right circular cone.

Answer 1

Hint:It is given in the question that the right-angled triangle PQR revolves around the side QR to form a regular solid cone. Since QR is the axis of revolution for forming the cone, it becomes the height of the solid cone. The side PQ of the triangle PQR becomes the radius of the base of the solid cone. By using these two parameters - height of cone and radius of base we need to calculate the
volume of the cone.

Complete step by step solution:
In the right-angled triangle PQR, PQ = 12 cm, QR = 9 cm

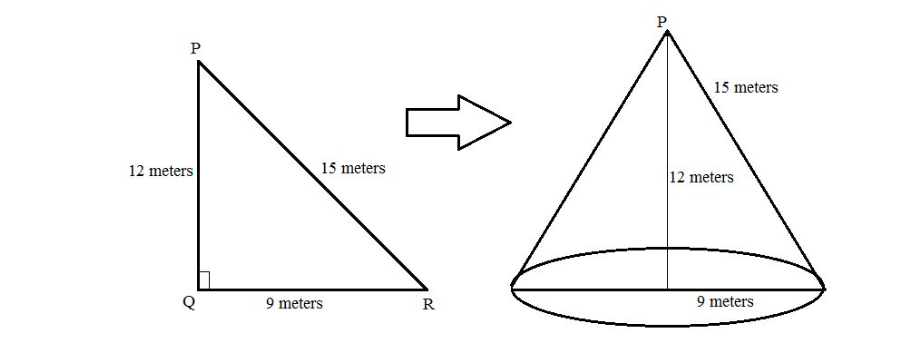
Now as the triangle PQR is rotated about the side PQ, PQ becomes the vertical height of the solid cone and the side QR becomes the radius of the circular base of the solid cone. From the above figure, we can see that the data for the height and the base-radius of the cone is provided. To calculate the volume of the cone we use the formula;

Volume of cone = \[\dfrac{1}{3}\pi {r^2}h\] [ where r is the base radius of cone and h is the height]

According to the question, r=12 cm and h= 9 cm.
\[\therefore \]Volume of the cone = \[\dfrac{1}{3}\pi {(12)^2}(9)\] = 1357.16 \[c{m^2}\]
Hence the volume of the solid comes out to be 1357.16 \[c{m^2}\].

Formula used:The formula used here is the volume of a solid cone V= \[\dfrac{1}{3}\pi {r^2}h\]

Note:Be very careful while using the formulas as most of the formulas are bit similar to each other, Secondary be very careful while choosing the height and radius. In this question we have been given that it must be revolved along RQ so PQ becomes the radius.

This is the reason why we have rotated out the figure above(to make PQ as the base so it can be the radius after formation of cones) or else QR would have become the radius which would be completely wrong.