Question

It is given that in $\Delta ABC,\overrightarrow {AD} $ is a median, hence according to the Apollonius theorem which one of the following results is true?
A)$A{B^2} + A{C^2} = 2\left( {A{D^2} + B{C^2}} \right)$
B)$A{B^2} + A{C^2} = 2\left( {B{D^2} + D{C^2}} \right)$
C)$A{B^2} + A{C^2} = 2\left( {A{D^2} + D{C^2}} \right)$
D)$A{B^2} + A{C^2} = 2\left( {B{D^2} + B{C^2}} \right)$

Answer 1

Hint- In this question, we have to apply Apollonius theorem, which states that the sum of squares of any two sides of a triangle equals twice its square on half of the third side along with twice of its square on the median bisecting the third side. For this we will make use of the Pythagoras theorem on sub right-angled triangles.

Complete step-by-step answer:

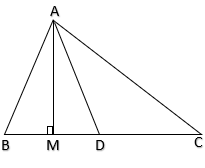
Let AM be perpendicular to BC and AD be median to BC such

that $BD = CD = \dfrac{{BC}}{2}$ ---(A)

Using the Pythagorean theorem, which simply states that in a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides. The sides of this triangle have been named as Perpendicular, Base and Hypotenuse. Here, the hypotenuse is the longest side, as it is opposite to the angle 90°.

${H^2} = {P^2} + {B^2}$ where H = Hypotenuse, P = Perpendicular, B = Base

Here, Using Pythagorean theorem we get in $\Delta AMB$

$ \Rightarrow A{B^2} = A{M^2} + B{M^2}$ ---(1)

Using Pythagorean theorem in $\Delta AMD$

$ \Rightarrow A{D^2} = A{M^2} + M{D^2}$ ----(2)

Using Pythagorean theorem in $\Delta AMC$

$ \Rightarrow A{C^2} = A{M^2} + M{C^2}$ ----(3)

Adding (1) and (3)

$ \Rightarrow A{B^2} + A{C^2} = 2A{M^2} + M{C^2} + B{M^2}$

          $ = 2A{M^2} + M{C^2} + B{M^2} + 2D{M^2} - 2D{M^2}$

          $ = 2A{M^2} + 2D{M^2} + M{C^2} - D{M^2} + B{M^2} - D{M^2}$

Taking 2 common from the first two terms and applying ${a^2} - {b^2} = (a + b)(a - b)$ on the other terms separately.

          $ = 2(A{M^2} + D{M^2}) + (MC + DM)(MC - DM) + (BM + DM)(BM - DM)$

Using (2) here for the first two terms and also, we know that MC – DM = DC and BM + DM =

BD

           $ = 2(A{M^2} + D{M^2}) + (MC + DM)DC + BD(BM - DM)$

Now using (A) here we get,

          $ = 2A{D^2} + (MC + DM)DC + DC(BM - DM)$

          $ = 2A{D^2} + DC(MC + BM)$

Also, MC + BM = BC from the figure above

          \[ = 2A{D^2} + DC \times BC\]

Again using (A) which states that $DC = \dfrac{{BC}}{2}$ or $BC = 2DC$

          $ = 2A{D^2} + DC \times 2DC$

          $ = 2A{D^2} + 2D{C^2}$

Taking 2 common from both we get,

$ \Rightarrow A{B^2} + A{C^2} = 2(A{D^2} + D{C^2})$

Hence, $A{B^2} + A{C^2} = 2(A{D^2} + D{C^2})$

$\therefore $ Option C. is the correct answer.


Note- In these types of questions, always try to use Pythagorean theorem which simply states that in a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides to suitable triangles and arrange the results to find the answer.