Question

Is parallelogram a rectangle? Can you call a rectangle a parallelogram?

Answer 1

Hint: From the given question, we have to discuss only the geometrical shapes of a rectangle and a parallelogram. First, we have to discuss some properties of a rectangle and properties of a parallelogram.

Complete step-by-step answer:
For the result, first we have to discuss some properties of a rectangle and properties of a parallelogram.
A rectangle is a quadrilateral with four right angles. It can also be defined as an equiangular quadrilateral, since equiangular means that all of its angles are equal$\left( {\dfrac{{{{360}^ \circ }}}{4} = {{90}^ \circ }} \right)$. It can also be defined as a parallelogram containing a right angle.

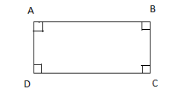
Properties of a rectangle are given below:
$1.$ A rectangle has four sides, four vertices and four angles.
$2.$ Opposite sides are congruent. \[\overline {{\text{AB}}} \cong \overline {{\text{DC}}} \], \[\overline {{\text{AD}}} \cong \overline {{\text{BC}}} \].
$3.$ Adjacent sides are perpendicular.\[\overline {{\text{AB}}} \bot \overline {{\text{BC}}} \],\[\overline {{\text{BC}}} \bot \overline {{\text{CD}}} \],\[\overline {{\text{CD}}} \bot \overline {{\text{DA}}} \],\[\overline {{\text{DA}}} \bot \overline {{\text{AB}}} \].
$4.$ Opposite sides are parallel.\[\overline {{\text{AB}}} \parallel \overline {{\text{DC}}} \],\[\overline {{\text{AD}}} \parallel \overline {{\text{BC}}} \].
A parallelogram is a quadrilateral with both pairs of opposite sides parallel. In a quadrilateral, opposite sides do not share a vertex and opposite angles do not share a side.

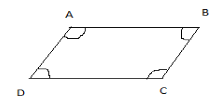
Properties of a parallelogram are given below:
$1.$ The diagonals of a parallelogram bisect each other.
$2.$ Opposite angles of a parallelogram are congruent.
$3.$ Opposite sides of a parallelogram are congruent.
$4.$ Each diagonal bisects the parallelogram into two congruent triangles. That is, any two adjacent angles add up to ${180^ \circ }$.
$\angle {\text{A}} + \angle {\text{B}} = {180^ \circ }$, \[\angle {\text{B}} + \angle {\text{C}} = {180^ \circ }\],\[\angle {\text{C}} + \angle {\text{D}} = {180^ \circ }\],$\angle {\text{D}} + \angle {\text{A}} = {180^ \circ }$.
From the given question, now we are going to discuss only the geometrical shapes of a rectangle and a parallelogram.
From the above discussed properties of a rectangle and properties of a parallelogram, we are going to conclude the required first result in the following manner.
The main characteristic of a rectangle is that the opposite sides must be equal and all the angles must be ${90^ \circ }$. A parallelogram has opposite equal sides but the angles may not be ${90^ \circ }$.
$\therefore $ Every parallelogram cannot be rectangle.
Now, we are going to conclude the second result in the following manner.
The main characteristic of a parallelogram is that the opposite sides must be parallel to each other. In a rectangle the opposite sides are parallel to one another.
$\therefore $ Every rectangle is a parallelogram.
Therefore, we have to conclude the required result.

Yes, every parallelogram cannot be a rectangle but every rectangle is a parallelogram.

Note: A square is similar to a rectangle. Square has 4 sides and 2 internal diagonals with internal angles equal to 90. The only difference between square and rectangle is that, in a square all the sides are equal but in a rectangle only the opposite sides are equal.