Question

Inside a uniform spherical shell.
(A) The gravitational potential is zero
(B) The gravitational field is zero
(C) The gravitational potential is same everywhere
(D) All of these

Answer 1

Hint: When a body is placed inside a uniform spherical shell, the gravitational force on the body due to the spherical shell is zero.

Complete step by step solution:
If we take any point P inside a spherical shell having uniformly distributed mass on its surface as shown, and divide the sphere into two parts using a plane passing through the point P.

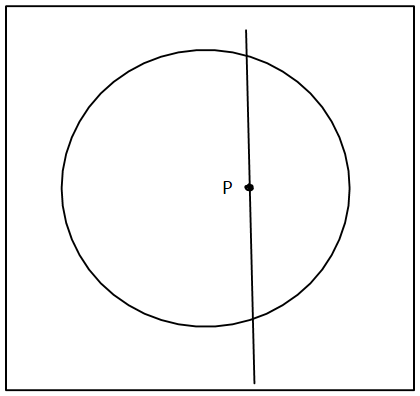
Then the gravitational field due to the left part at P will cancel the gravitational field due to the right part at P. Hence the gravitational field inside a sphere is zero at all points.

The gravitational potential difference between two points can be calculated using gravitational field from the following formula
\[dV = - \overrightarrow E .\overrightarrow {dr} \]

Since Electric field is zero at all points, we get

\[\Delta V = 0\]
This means that the gravitational potential difference between any two points is zero.
Hence all points inside a spherical shell are at same potential

Therefore, the correct answer to the question are options: B and C

Option A: The gravitational potential is zero, is incorrect because generally gravitational potential is considered to be zero at infinity and in that case gravitational potential inside a spherical shell is non zero.

Note: Before attempting to solve the problem, the student needs to be able to understand the derivation of gravitational fields inside a hollow sphere using integration and considering a small ring element on the surface of the spherical shell.
Another important point to be noted here is, the gravitational potential can be assumed to be zero inside the spherical shell also, and in that case Option D will be correct, but since it was not mentioned that gravitational potential is to be assumed zero inside, we will consider the more general/common approach and that is to consider it zero at infinity.