Question

In YDSC there is a point P on the screen. What is path difference at point P. Given $d = 1mm, y = 2mm, D = 1m$

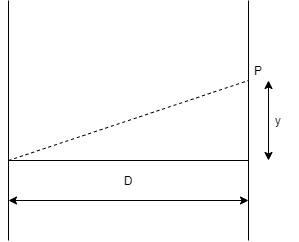
Answer 1

Hint: The path difference is defined as the difference in the distance traveled by the two waves from their source to a given point. In this figure, if we consider O as the point of origin for the two waves, the path difference is given by,
$P.D = OP - D$

Complete step by step answer:
Consider Young’s double-slit experiment as shown in the above figure

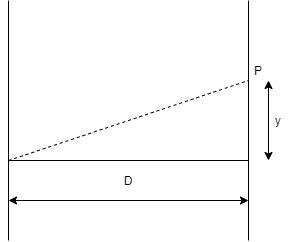
We see in this given figure that there is no presence of the slits as the dotted line at P actually, represents the path difference. By writing the actual figure denoting the two slits and the two wavefronts individually, we get a modified diagram like this,

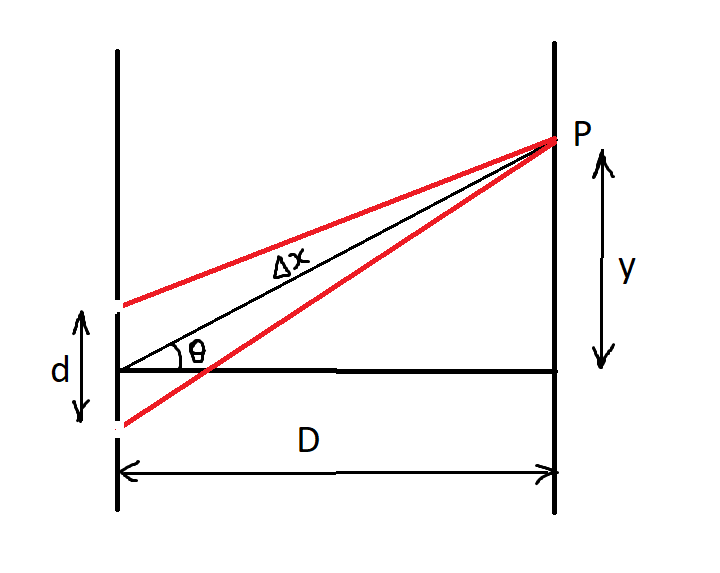
$\theta $ is the angle between the path difference and the horizontal reference line as shown.
The path difference, $\Delta x = d\sin \theta $
Since the angle $\theta $ is very small, we can say that, $\sin \theta = \tan \theta $
Substituting, we get,
$\Delta x = d\tan \theta $
From the figure, $\tan \theta = \dfrac{y}{D}$
Thus, substituting the value of $\tan \theta $, we get,
$
\Delta x = d\tan \theta \\
\Rightarrow \Delta x = d \times \dfrac{y}{D} \\
 $
Substituting the values, we get
$
\Delta x = d \times \dfrac{y}{D} \\
\Rightarrow \Delta x = 1 \times \dfrac{2}{{1000}} \\
\Rightarrow \Delta x = 2 \times {10^{ - 3}}mm \\
\Rightarrow \Delta x = 2\mu m \\
 $
Hence, the path difference, $\Delta x = 2\mu m$

Note:
At point P, there are two things that could happen. Either a bright fringe can be formed at the point of a dark fringe that can be formed at the point. The criteria for deciding this is solely, based on the path difference at that point.
If the path difference is equal to even multiples of $\dfrac{\lambda }{2}$ such as $\lambda, 2\lambda, 3\lambda ...2n\dfrac{\lambda }{2}$, there is a constructive interference at this point and we obtain a bright fringe.
If the path difference is equal to odd multiples of $\dfrac{\lambda }{2}$ such as $\dfrac{\lambda }{2},\dfrac{{3\lambda }}{2},\dfrac{{5\lambda }}{2}...\left( {2n + 1} \right)\dfrac{\lambda }{2}$, there is a destructive interference at this point and we obtain a dark fringe.